题目内容
6.已知二次函数f(x)=ax2+bx+1(a,b∈R),若f(-1)=0,且对任意x均有f(x)≥0恒成立,则实数a=1.分析 把函数f(x)=ax2+bx+1(a、b∈R)满足:f(-1)=0,代入可以求得a与b的关系式,再根据对任意实数x均有f(x)≥0成立,可以求出a与b的关系式;
解答 解:函数f(x)=ax2+bx+1(a、b∈R)满足:f(-1)=0,可得a-b+1=0,可得b=a+1
∵对任意实数x均有f(x)≥0成立,
∴ax2+bx+1=ax2+(a+1)x+1≥0,恒成立,
∴$\left\{\begin{array}{l}a>0\\△=(a+1)^{2}-4a≤0\end{array}\right.$,解得(a+1)2-4a=(a-1)2≤0,
∴a=1,b=2;
故答案为:1.
点评 此题主要考查二次函数的性质以及函数的恒成立问题,考查的知识点比较单一,是一道中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
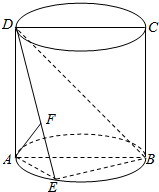 如图,圆柱轴截面ABCD是正方形,E是底面圆周上不同于A、B的一点,AF⊥DE于F.
如图,圆柱轴截面ABCD是正方形,E是底面圆周上不同于A、B的一点,AF⊥DE于F.