题目内容
14.若关于x的不等式|x|+|x-1|>|x-a|对?x∈R恒成立,则a的取值范围是(0,1).分析 令f(x)=|x|+|x-1|=$\left\{\begin{array}{l}{1-2x,x<0}\\{1,0≤x<1}\\{2x-1,x≥1}\end{array}\right.$,g(x)=|x-a|,由题意可得,函数f(x)的图象(如图实线部分)在函数g(x)(图中虚线部分)的上方,数形结合求得a的范围.
解答  解:令f(x)=|x|+|x-1|=$\left\{\begin{array}{l}{1-2x,x<0}\\{1,0≤x<1}\\{2x-1,x≥1}\end{array}\right.$,g(x)=|x-a|,
解:令f(x)=|x|+|x-1|=$\left\{\begin{array}{l}{1-2x,x<0}\\{1,0≤x<1}\\{2x-1,x≥1}\end{array}\right.$,g(x)=|x-a|,
由题意可得,函数f(x)的图象(如图实线部分)在函数g(x)(图中虚线部分)的上方,
故有0<a<1,
故答案为:(0,1).
点评 本题主要考查带有绝对值的函数,函数的恒成立问题,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
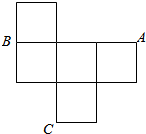 如图是一个无盖的正方体盒子展开后的平面图,A,B,C展开图是上的三点,则在正方体盒子中,∠ABC=90°.
如图是一个无盖的正方体盒子展开后的平面图,A,B,C展开图是上的三点,则在正方体盒子中,∠ABC=90°.