题目内容
已知 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )
 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )A. | B. | C. | D. |
D
试题分析:∵
 在
在 上递增,∴
上递增,∴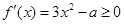 在
在 恒成立,即
恒成立,即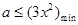 ,又函数
,又函数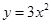 在
在 单调递减,故当x=-1时,函数
单调递减,故当x=-1时,函数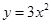 有最小值3,故
有最小值3,故 ,选D
,选D点评:注意在某区间内
 是函数
是函数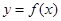 在该区间内为增(减)函数的充分非必要条件.
在该区间内为增(减)函数的充分非必要条件.
练习册系列答案
相关题目
题目内容
 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )A. | B. | C. | D. |
 在
在 上递增,∴
上递增,∴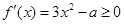 在
在 恒成立,即
恒成立,即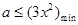 ,又函数
,又函数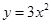 在
在 单调递减,故当x=-1时,函数
单调递减,故当x=-1时,函数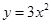 有最小值3,故
有最小值3,故 ,选D
,选D 是函数
是函数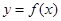 在该区间内为增(减)函数的充分非必要条件.
在该区间内为增(减)函数的充分非必要条件.