题目内容
已知函数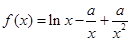 (
(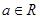 ).
).
(1)若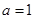 ,求函数
,求函数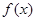 的极值;
的极值;
(2)若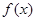 在
在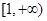 内为单调增函数,求实数a的取值范围;
内为单调增函数,求实数a的取值范围;
(3)对于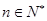 ,求证:
,求证: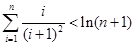 .
.
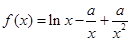 (
(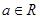 ).
).(1)若
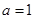 ,求函数
,求函数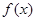 的极值;
的极值;(2)若
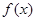 在
在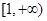 内为单调增函数,求实数a的取值范围;
内为单调增函数,求实数a的取值范围;(3)对于
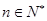 ,求证:
,求证: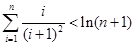 .
. (1) 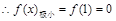 ,无极大值 (2)
,无极大值 (2) 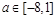 (3)见解析
(3)见解析
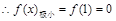 ,无极大值 (2)
,无极大值 (2) 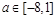 (3)见解析
(3)见解析(1)求出函数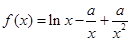 的导数,令导函数大于(小于)0,得函数的增(减)区间,也得到函数的极值点和极值;(2)
的导数,令导函数大于(小于)0,得函数的增(减)区间,也得到函数的极值点和极值;(2)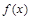 在
在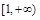 上单调递增, 就是
上单调递增, 就是
 在
在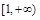 上恒成立.即
上恒成立.即 在
在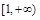 上恒成立。可直接利用二次函数的性质求
上恒成立。可直接利用二次函数的性质求 的最小值大于等于0,也可分离参数求最值;
的最小值大于等于0,也可分离参数求最值;
(3)由(1)知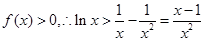 。结合要证结论令
。结合要证结论令 ,则有
,则有 。左右两边分别相加,再由对数的运算法则化简可证出结论
。左右两边分别相加,再由对数的运算法则化简可证出结论

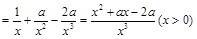
(1)若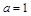 ,
,
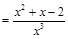 ,令
,令 =0,得
=0,得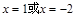 (负值舍去)
(负值舍去)
令 >0
>0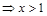 ,
, <0
<0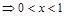
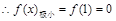 ,无极大值
,无极大值
(2) 在
在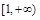 上单调递增,
上单调递增,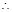

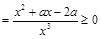 在
在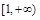 上恒成立.
上恒成立.
即 在
在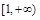 上恒成立.令
上恒成立.令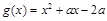
当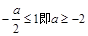 时,
时,

当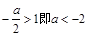 时,
时,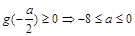

综上: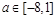
(3)当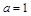 时,由(2)知,
时,由(2)知,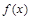 在
在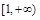 上单调递增
上单调递增
即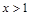 时,
时, ,
,
即
取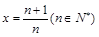 ,
,
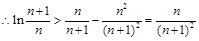
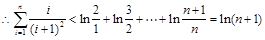
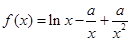 的导数,令导函数大于(小于)0,得函数的增(减)区间,也得到函数的极值点和极值;(2)
的导数,令导函数大于(小于)0,得函数的增(减)区间,也得到函数的极值点和极值;(2)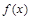 在
在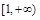 上单调递增, 就是
上单调递增, 就是
 在
在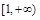 上恒成立.即
上恒成立.即 在
在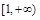 上恒成立。可直接利用二次函数的性质求
上恒成立。可直接利用二次函数的性质求 的最小值大于等于0,也可分离参数求最值;
的最小值大于等于0,也可分离参数求最值;(3)由(1)知
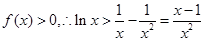 。结合要证结论令
。结合要证结论令 ,则有
,则有 。左右两边分别相加,再由对数的运算法则化简可证出结论
。左右两边分别相加,再由对数的运算法则化简可证出结论
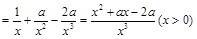
(1)若
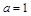 ,
,
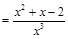 ,令
,令 =0,得
=0,得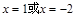 (负值舍去)
(负值舍去)令
 >0
>0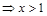 ,
, <0
<0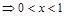
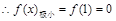 ,无极大值
,无极大值(2)
 在
在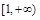 上单调递增,
上单调递增,

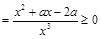 在
在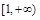 上恒成立.
上恒成立.即
 在
在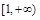 上恒成立.令
上恒成立.令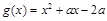
当
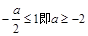 时,
时,

当
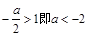 时,
时,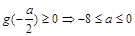

综上:
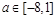
(3)当
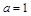 时,由(2)知,
时,由(2)知,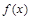 在
在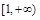 上单调递增
上单调递增即
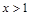 时,
时, ,
,即

取
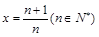 ,
,
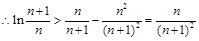
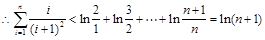

练习册系列答案
相关题目
 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )



 已知
已知 在
在 时取得极值,则
时取得极值,则 等于( )
等于( )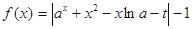
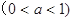 有零点,则实数
有零点,则实数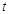 的最小值是( )
的最小值是( ) 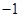
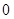

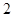
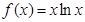 ,
,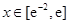 ,则
,则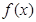 的最大值为____________,最小值为___________.
的最大值为____________,最小值为___________. 有( )
有( ) ,极小值
,极小值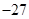

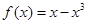 在
在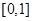 上的最大值为( )
上的最大值为( )



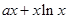 的图像在点
的图像在点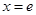 (
(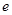 为自然常数)处的切线斜率为3.
为自然常数)处的切线斜率为3.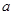 的值
的值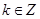 ,且
,且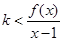 对任意的
对任意的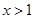 恒成立,求
恒成立,求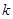 得最大值
得最大值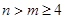 时,证明
时,证明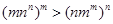
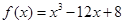 在区间
在区间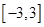 上的最大值与最小值分别为
上的最大值与最小值分别为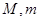 ,
,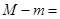 _____________________________;
_____________________________;