题目内容
设直线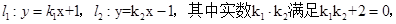
(I)证明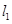 与
与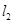 相交;
相交;
(II)证明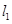 与
与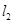 的交点在椭圆
的交点在椭圆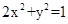 上.
上.
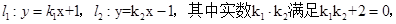
(I)证明
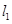 与
与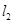 相交;
相交;(II)证明
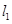 与
与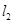 的交点在椭圆
的交点在椭圆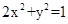 上.
上.见解析
(1)(反证法)假设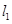 与
与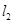 不相交,则
不相交,则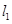 与
与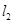 必平行,
必平行,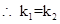 代入
代入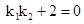 得
得
 ,与
,与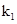 是实数相矛盾。从而
是实数相矛盾。从而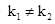 ,即
,即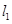 与
与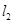 相交。
相交。
(2)(方法一)由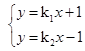 得交点p的坐标(x,y)为
得交点p的坐标(x,y)为
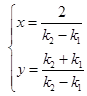 ,
,
而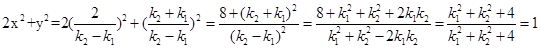
所以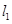 与
与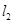 的交点p的(x,y)在椭圆
的交点p的(x,y)在椭圆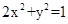 上
上
(方法二)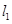 与
与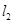 的交点p的(x,y)满足:
的交点p的(x,y)满足: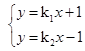 ,
,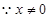 ,从而
,从而
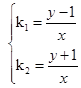 ,代入
,代入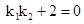 得
得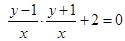 ,整理得
,整理得
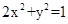
所以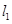 与
与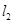 的交点p的(x,y)在椭圆
的交点p的(x,y)在椭圆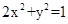 上
上
两直线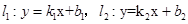 的位置关系判定方法:
的位置关系判定方法:
(1)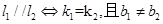
(2)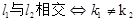
(3)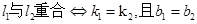
证明两数不等可采用反证法的思路。
点在线上的判断与证明只要将点的坐标代入曲线方程判断其是否成立即可,或求出交点的轨迹方程并判断与所给的曲线方程是否一致即可。本题属于中档题。
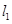 与
与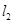 不相交,则
不相交,则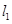 与
与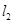 必平行,
必平行,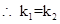 代入
代入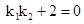 得
得 ,与
,与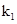 是实数相矛盾。从而
是实数相矛盾。从而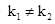 ,即
,即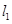 与
与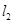 相交。
相交。(2)(方法一)由
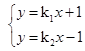 得交点p的坐标(x,y)为
得交点p的坐标(x,y)为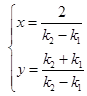 ,
,而
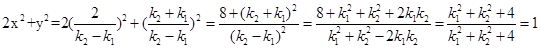
所以
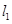 与
与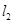 的交点p的(x,y)在椭圆
的交点p的(x,y)在椭圆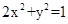 上
上(方法二)
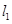 与
与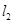 的交点p的(x,y)满足:
的交点p的(x,y)满足: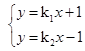 ,
, ,从而
,从而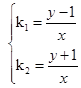 ,代入
,代入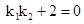 得
得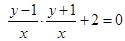 ,整理得
,整理得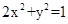
所以
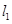 与
与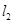 的交点p的(x,y)在椭圆
的交点p的(x,y)在椭圆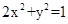 上
上两直线
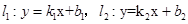 的位置关系判定方法:
的位置关系判定方法:(1)
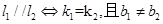
(2)
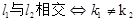
(3)
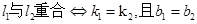
证明两数不等可采用反证法的思路。
点在线上的判断与证明只要将点的坐标代入曲线方程判断其是否成立即可,或求出交点的轨迹方程并判断与所给的曲线方程是否一致即可。本题属于中档题。

练习册系列答案
相关题目
 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且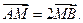
 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线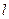 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上
上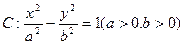 与椭圆
与椭圆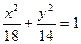 有共同的焦点,点
有共同的焦点,点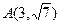 在双曲线C上.
在双曲线C上. 所表示的曲线为
所表示的曲线为 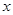 轴上的椭圆
轴上的椭圆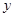 轴上的椭圆
轴上的椭圆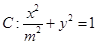 (常数
(常数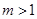 ),点
),点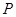 是
是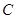 上的动点,
上的动点,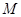 是右顶点,定点
是右顶点,定点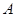 的坐标为
的坐标为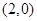 。
。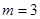 ,求
,求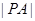 的最大值与最小值;
的最大值与最小值;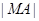 ,求
,求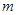 的取值范围。
的取值范围。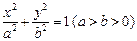 的左、右焦点,点P(-1,
的左、右焦点,点P(-1,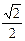 )在椭圆上,线段PF2与
)在椭圆上,线段PF2与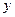 轴的交点
轴的交点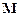 满足
满足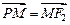 .(1)求椭圆的标准方程;
.(1)求椭圆的标准方程; 轴重合的直线
轴重合的直线 ,
,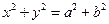 相交于A、B.并与椭圆相交于C、D.当
相交于A、B.并与椭圆相交于C、D.当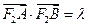 ,且
,且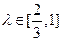 时,求△F2CD的面积S的取值范围.
时,求△F2CD的面积S的取值范围.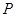 为双曲线
为双曲线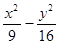 =1的右支上一点,
=1的右支上一点,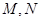 分别是圆
分别是圆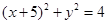 和
和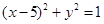 上的点,则
上的点,则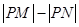 的最大值为
的最大值为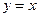 与抛物线C相交
与抛物线C相交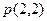 是AB的中点,则抛物线C的方程为_______________.
是AB的中点,则抛物线C的方程为_______________.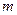 为常数,若点
为常数,若点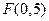 是双曲线
是双曲线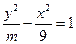 的一个焦点,则
的一个焦点,则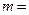 。
。