题目内容
(本题16分,第(1)小题3分;第(2)小题5分;第(3 )小题8分)
)小题8分)
已知数列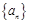 和
和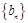 的通项分别为
的通项分别为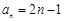 ,
,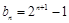 (
(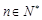 ),集合
),集合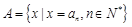 ,
,
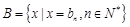 ,设
,设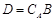 . 将集合
. 将集合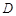 中元素从小到大依次排列,构成数列
中元素从小到大依次排列,构成数列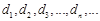 .
.
(1)写出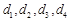 ;
;
(2)求数列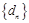 的前
的前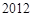 项的和;
项的和;
(3)是否存在这样的无穷等差数列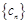 :使得
:使得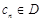 (
(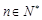 )?若存在,请写出一个这样的
)?若存在,请写出一个这样的
数列,并加以证明;若不存在,请说明理由.
 )小题8分)
)小题8分)已知数列
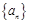 和
和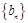 的通项分别为
的通项分别为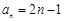 ,
,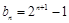 (
(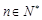 ),集合
),集合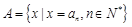 ,
,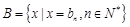 ,设
,设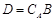 . 将集合
. 将集合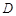 中元素从小到大依次排列,构成数列
中元素从小到大依次排列,构成数列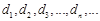 .
.(1)写出
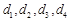 ;
;(2)求数列
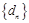 的前
的前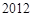 项的和;
项的和;(3)是否存在这样的无穷等差数列
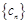 :使得
:使得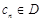 (
(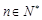 )?若存在,请写出一个这样的
)?若存在,请写出一个这样的数列,并加以证明;若不存在,请说明理由.
(1)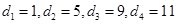
(错1个扣1分)
(2)
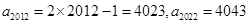 ,
,
所以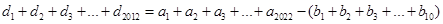
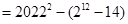
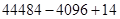
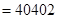
(3)存在。如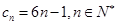 ,
,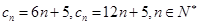 (不唯一)
(不唯一)
(结论1分,通项2分
证明: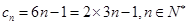 ,所
,所 以
以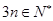 ,所以
,所以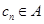
假设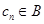 ,则存在实数
,则存在实数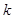 ,
,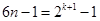 ,所以
,所以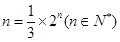 ,由于上式左边为整数,右边为分数,所以上式不成立,所以假设不成立,所以
,由于上式左边为整数,右边为分数,所以上式不成立,所以假设不成立,所以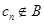
所以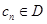 。即:
。即: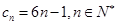 满足要求。
满足要求。
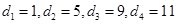
(错1个扣1分)
(2)

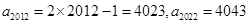 ,
,所以
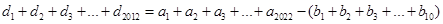
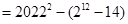
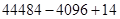
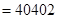
(3)存在。如
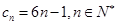 ,
,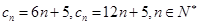 (不唯一)
(不唯一)(结论1分,通项2分
证明:
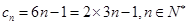 ,所
,所 以
以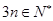 ,所以
,所以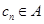
假设
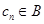 ,则存在实数
,则存在实数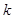 ,
,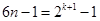 ,所以
,所以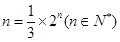 ,由于上式左边为整数,右边为分数,所以上式不成立,所以假设不成立,所以
,由于上式左边为整数,右边为分数,所以上式不成立,所以假设不成立,所以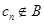
所以
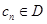 。即:
。即: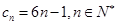 满足要求。
满足要求。略

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 中,
中,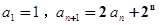
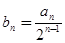 ,证明:数列
,证明:数列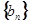 是等差数列。
是等差数列。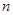 项和
项和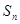 。
。 的前
的前 项和为
项和为 ,且
,且 ,则( )
,则( )



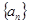 满足
满足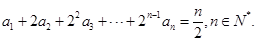
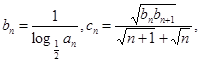 记
记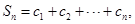 证明:Sn<1.
证明:Sn<1.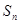 是数列
是数列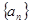 的前
的前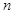 项和,
项和,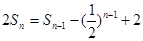 (
(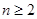 ,
,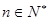 ),且
),且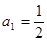 .
.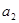 的值,并写出
的值,并写出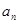 和
和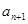 的关系式;
的关系式; 3)我们可以证明:若数列
3)我们可以证明:若数列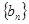 有上界(即存在常数
有上界(即存在常数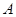 ,使得
,使得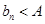 对一切
对一切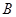 ,使得
,使得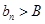 对一切
对一切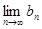 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: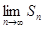 存在.
存在. 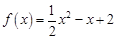 ,数列
,数列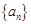 满足递推关系式:
满足递推关系式: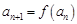 (
(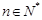 ),且
),且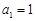 、
、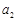 、
、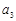 、
、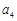 的值;
的值; 时,
时,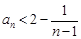 ;
;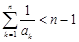 、
、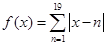 的最小值为
的最小值为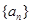 满足性质“对任意正整数
满足性质“对任意正整数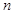 ,
,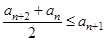 都成立”且
都成立”且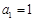 ,
,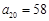 ,则
,则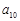 的最小值为
的最小值为 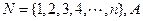 为非空集合,且
为非空集合,且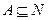 ,定义
,定义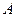 的“交替和”如下:将集合
的“交替和”如下:将集合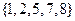 的交替和为8-7+5-2+1=5,集合
的交替和为8-7+5-2+1=5,集合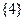 的交替和为4,当
的交替和为4,当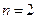 时,集合
时,集合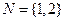 的非空子集为
的非空子集为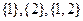 ,记三个集合的交替和的总和为
,记三个集合的交替和的总和为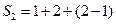 = 4,则
= 4,则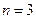 时,集合
时,集合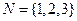 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和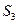 = ;集合
= ;集合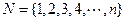 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和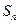 =
=