题目内容
【题目】如图,在正方体![]() 中,点
中,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上的动点,下列说法中:
上的动点,下列说法中:
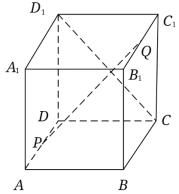
①![]() 可能与平面
可能与平面![]() 平行;
平行;
②![]() 与
与![]() 所成的角的最大值为
所成的角的最大值为![]() ;
;
③![]() 与
与![]() 一定垂直;
一定垂直;
④![]()
⑤![]() 与
与![]() 所成的最大角的正切值为
所成的最大角的正切值为![]() .
.
其中正确个数为( )
A.2B.3C.4D.5
【答案】C
【解析】
结合空间中线线、线面、面面间的位置关系及正方体的性质,对题中5个说法逐个分析,可选出答案.
对于①,当![]() 为
为![]() 的中点时,因为
的中点时,因为![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,又因为
,又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故①正确;
,故①正确;
对于②,当![]() 为
为![]() 的中点时,
的中点时, ![]() ,又
,又![]() ,
,![]() ,可得
,可得![]() ,此时
,此时![]() 与
与![]() 所成的角为
所成的角为![]() ,故②错误;
,故②错误;
对于③,由![]() ,
,![]() ,且
,且![]() ,可得
,可得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,故
,故![]() ,故③正确;
,故③正确;
对于④,当![]() 为
为![]() 的中点时,线段
的中点时,线段![]() 的长为两平行线
的长为两平行线![]() 之间的距离,且
之间的距离,且![]() ,故
,故![]() ,即④正确;
,即④正确;
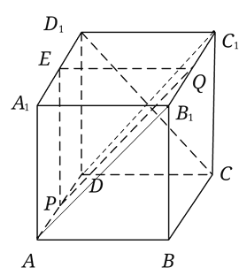
对于⑤,如图,点![]() 为
为![]() 中点,连结
中点,连结![]() ,因为
,因为![]() ,所以
,所以![]() 与
与![]() 所成角的正切值即为
所成角的正切值即为![]() 与
与![]() 所成角的正切值,为
所成角的正切值,为![]() ,点
,点![]() 为
为![]() 上移动,
上移动,![]() 始终为直角三角形,当
始终为直角三角形,当![]() 与
与![]() 或
或![]() 重合时,
重合时,![]() 取得最大值,此时
取得最大值,此时![]() 与
与![]() 所成角的正切值最大,且
所成角的正切值最大,且![]() 与
与![]() 所成的角也最大,设正方体边长为2,则
所成的角也最大,设正方体边长为2,则![]() ,
,![]() ,所以所成最大角的正切值为
,所以所成最大角的正切值为![]() ,故⑤正确.
,故⑤正确.
所以正确的个数为4.
故选:C.

练习册系列答案
相关题目