题目内容
6.在△ABC中,a=4,b=5,c=6,则$\frac{sin2A}{sinC}$=1.分析 利用余弦定理求出cosC,cosA,即可得出结论.
解答 解:∵△ABC中,a=4,b=5,c=6,
∴cosC=$\frac{16+25-36}{2×4×5}$=$\frac{1}{8}$,cosA=$\frac{25+36-16}{2×5×6}$=$\frac{3}{4}$
∴sinC=$\frac{3\sqrt{7}}{8}$,sinA=$\frac{\sqrt{7}}{4}$,
∴$\frac{sin2A}{sinC}$=$\frac{2×\frac{\sqrt{7}}{4}×\frac{3}{4}}{\frac{3\sqrt{7}}{8}}$=1.
故答案为:1.
点评 本题考查余弦定理,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A. | 若m⊥α,α⊥β,则m∥β | B. | 若m⊥n,n⊥β,则m∥β | ||
| C. | 若m⊥α,α⊥β,m与n异面,则n与β相交 | D. | 若m⊥α,n⊥β,m与n异面,则α与β相交 |
17.下列双曲线中,焦点在y轴上且渐近线方程为y=±2x的是( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-y2=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-$\frac{{x}^{2}}{4}$=1 |
11.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为( )
| A. | 0.4 | B. | 0.6 | C. | 0.8 | D. | 1 |
16.袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )
| A. | $\frac{5}{21}$ | B. | $\frac{10}{21}$ | C. | $\frac{11}{21}$ | D. | 1 |
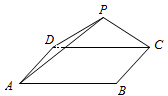 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3. 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,