题目内容
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量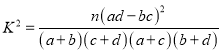 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
【答案】(1)分布列见解析, ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)分层从![]() 份女生问卷中抽取了
份女生问卷中抽取了![]() 份问卷,其中“科学用眼”抽
份问卷,其中“科学用眼”抽![]() 人,“不科学用眼”抽
人,“不科学用眼”抽![]() 人,若从这
人,若从这![]() 份问卷中随机抽取
份问卷中随机抽取![]() 份,随机变量
份,随机变量![]() .利用“超几何分布”即可得出分布列及其数学期望;(2)根据“独立性检验的基本思想的应用”计算公式可得
.利用“超几何分布”即可得出分布列及其数学期望;(2)根据“独立性检验的基本思想的应用”计算公式可得![]() 的观测值
的观测值![]() ,即可得出.
,即可得出.
试题解析:(1)“科学用眼”抽![]() 人,“不科学用眼”抽
人,“不科学用眼”抽![]() 人.
人.
则随机变量![]() ,
,
∴![]() ,
,![]() ,
,![]()
分布列为
| 0 | 1 | 2 |
|
|
|
|
![]()
(2)![]()
由表可知2.706<3.030<3.840;
∴![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】某市![]() 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
中学 |
|
|
|
|
人数 |
|
|
|
|
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查.
(1)问![]() 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?
(2)在参加问卷调查的![]() 名学生中,从来自
名学生中,从来自![]() 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用![]() 表示抽得
表示抽得![]() 中学的学生人数,求
中学的学生人数,求![]() 的分布列,数学期望和方差.
的分布列,数学期望和方差.