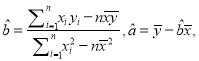题目内容
【题目】已知椭圆![]() 的顶点
的顶点![]() 到左焦点
到左焦点![]() 的距离为
的距离为![]() ,离心率
,离心率![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 的右頂点,过点
的右頂点,过点![]() 作互相垂直的两条射线,与椭圆
作互相垂直的两条射线,与椭圆![]() 分別交于不同的两点
分別交于不同的两点![]() 不与左、右顶点重合) ,试判断直线
不与左、右顶点重合) ,试判断直线![]() 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)直线过定点
;(2)直线过定点![]() .
.
【解析】
试题分析:(1)根据题意列出![]() 的方程组结合
的方程组结合![]() ,求出
,求出![]() 的值;(2)当直线
的值;(2)当直线![]() 的斜率不存在时,求出
的斜率不存在时,求出![]() 两点坐标,可得其与
两点坐标,可得其与![]() 的交点,当当直线的斜率存在时,设直线
的交点,当当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,整理方程组可得
,整理方程组可得![]() 两点坐标的关系,根据
两点坐标的关系,根据![]() 及椭圆的右顶点
及椭圆的右顶点![]()
![]() ,由向量的数量积坐标表示出
,由向量的数量积坐标表示出![]() 的关系,代入直线方程即可求得直线经过的定点.
的关系,代入直线方程即可求得直线经过的定点.
试题解析:(1)由题意可知: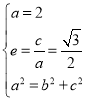 , 解得:
, 解得:![]() ,故椭圆的标准方程为
,故椭圆的标准方程为![]() .
.
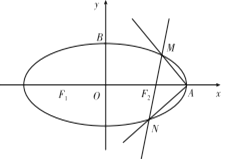
(2)设![]() 当直线
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 轴,
轴,![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,又
,又![]() ,又
,又![]() 不与左、右顶点重合,解得
不与左、右顶点重合,解得![]() ,此时,直线
,此时,直线![]() 过点
过点![]() .
.
当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,由方程组
,由方程组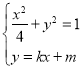 ,得
,得![]() ,整理得
,整理得![]() ,则
,则![]() .由已知
.由已知![]() ,且椭圆的右顶点
,且椭圆的右顶点![]() 为
为![]() ,所以
,所以![]() ,
,![]() ,即
,即![]() ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() 均满足
均满足![]() 成立.当
成立.当![]() 时,直线
时,直线![]() 的方程
的方程![]() 过顶点
过顶点![]() ,与题意矛盾舍去.当
,与题意矛盾舍去.当![]() 时,直线
时,直线![]() 的方程
的方程![]() 过定点
过定点![]() ,故直线过定点,且定点是
,故直线过定点,且定点是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】海州市英才中学某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分別到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是相邻两个月的概率;
组数据恰好是相邻两个月的概率;
(2)若选取的是![]() 月与6月的两组数据,请根据
月与6月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想.
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想.
其中回归系数公式, ,
,![]()
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量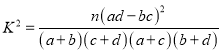 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |