题目内容
【题目】已知a,b,c是![]() ABC中角A,B,C的对边,S是
ABC中角A,B,C的对边,S是![]() ABC的面积.若a2+c2=b2+ac,
ABC的面积.若a2+c2=b2+ac,
(I)求角B ; (II)若b=2,S=![]() ,判断三角形形状
,判断三角形形状
【答案】(I)![]() ;(Ⅱ)等边三角.
;(Ⅱ)等边三角.
【解析】试题分析:
(1)利用题意首先求得![]() 的值,然后利用特殊角的三角函数值求解
的值,然后利用特殊角的三角函数值求解![]() 的大小即可;
的大小即可;
(2)利用三角形的面积公式确定![]() 即可确定△ABC为等边三角形.
即可确定△ABC为等边三角形.
试题解析:
(I)由![]() 得
得![]()
又因为![]()
所以![]()
又![]() 所以
所以![]()
(Ⅱ)![]() ,得
,得![]()
又![]() ,所以
,所以 ![]() ,得
,得![]()
故三角形为等边三角
点睛:在解三角形的问题中,三角形内角和定理起着重要作用,在解题时要注意根据这个定理确定角的范围及三角函数值的符号,防止出现增解或漏解.
正、余弦定理在应用时,应注意灵活性,尤其是其变形应用时可相互转化.如a2=b2+c2-2bccos A可以转化为sin2 A=sin2 B+sin2 C-2sin Bsin Ccos A,利用这些变形可进行等式的化简与证明.
判断三角形形状的两种途径,一是化边为角;二是化角为边,并常用正弦(余弦)定理实施边、角转换.

【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量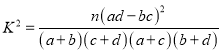 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |


