题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(1)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,当
,当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)因为函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() 恒成立,转化为二次函数
恒成立,转化为二次函数![]() 恒成立问题,得解;(2)令
恒成立问题,得解;(2)令![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 恒成立,利用导数讨论
恒成立,利用导数讨论![]() 的单调性求最值.
的单调性求最值.
试题解析:(1)因为函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() ,
,
即![]() 在
在![]() 上恒成立
上恒成立
当![]() 时,令
时,令![]() 得
得![]() ,
,
①若![]() ,则
,则![]() ,解得
,解得![]() ;②若
;②若![]() ,则
,则![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)令![]() ,则
,则![]() ,
,
根据题意,当![]() 时,
时, ![]() 恒成立.
恒成立.
所以![]() .
.
①当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符合题意
,所以不符合题意
②当![]() 时,
时, ![]() 时,
时, ![]() 恒成立.
恒成立.
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符题意.
,所以不符题意.
③当![]() 时,
时, ![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,
上是减函数,
于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,
,
即![]() ,解得
,解得![]() ,故
,故![]()
综上, ![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量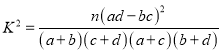 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |