题目内容
直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=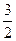 ,BC=
,BC=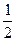 .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.
(1)建立适当坐标系,求椭圆C的方程;
(2)若点E满足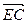
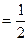
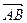 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且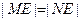 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由
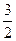 ,BC=
,BC=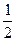 .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.(1)建立适当坐标系,求椭圆C的方程;
(2)若点E满足
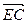
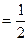
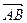 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且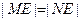 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由(1)
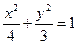
(2)(0,
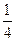 ]
](1)如图,以AB所在直线为x轴,AB中垂线y轴建立直角坐标系
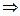 A(-1,0),B(1,0)
A(-1,0),B(1,0)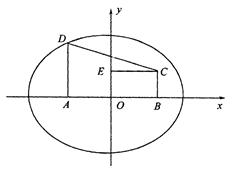
设椭圆方程为:
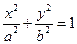
令
 ∴
∴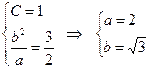
∴ 椭圆C的方程是:
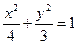 …………………………5分
…………………………5分(2)
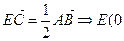 ,
,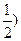 ,l⊥AB时不符,
,l⊥AB时不符,设l:y=kx+m(k≠0)
由
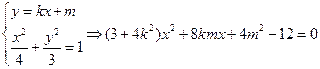
M、N存在
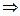 ?
?
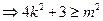
设M(
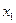 ,
,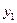 ),N(
),N(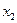 ,
,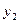 ),MN的中点F(
),MN的中点F(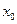 ,
, )
)∴
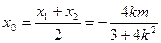 ,
,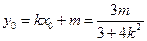
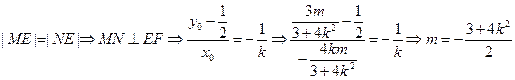
∴
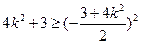 ∴
∴ ∴
∴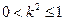 ∴
∴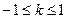 且
且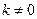
∴ l与AB的夹角的范围是(0,
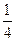 ].…………………………12分
].…………………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
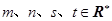 ,
,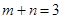 ,
,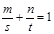 其中
其中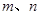 是常数且
是常数且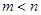 ,若
,若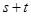 的最小值 是
的最小值 是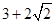 ,满足条件的点
,满足条件的点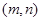 是椭圆
是椭圆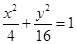 一弦的中点,则此弦所在的直线方程为
一弦的中点,则此弦所在的直线方程为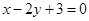
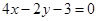
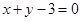
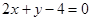
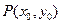 是椭圆
是椭圆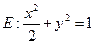 上任意一点
上任意一点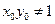 ,直线
,直线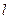 的方程为
的方程为
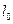 过P点与直线
过P点与直线 上一点,
上一点,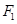 为椭圆的一个焦点,且
为椭圆的一个焦点,且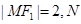 为线段
为线段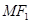 的中点,则ON的长为
的中点,则ON的长为 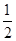
 上两点间最大的距离为8,则实数
上两点间最大的距离为8,则实数 的值是 ▲
的值是 ▲ 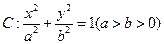 过点
过点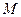 (
(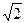
 ,1),且左焦点为
,1),且左焦点为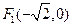 .
.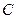 的方程;
的方程;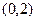 的直线
的直线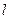 与椭圆
与椭圆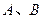 两点并且满足
两点并且满足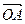 ·
·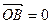 ,若存在求出直线
,若存在求出直线 :
: ,则“
,则“ ”是“曲线C表示焦点在
”是“曲线C表示焦点在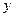 轴上的椭圆”的什么条件( )
轴上的椭圆”的什么条件( ) 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为
 且
且 ,则
,则 的最小值是 .
的最小值是 .