题目内容
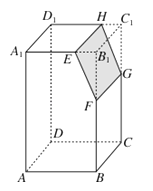
【题目】若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )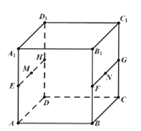
A.1
B.2
C.3
D.4
【答案】B
【解析】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD﹣A1B1C1D1中棱长为2,
∵E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,
∴M(1,0,1),N(1,2,1),E(2,0,1),G(0,2,1),
F(2,2,1),H(0,0,1),B1(2,2,2),D(0,0,0),
A1(2,0,2),D1(0,0,2),A(2,0,0),B(2,2,0),
则MN到AB的距离为AM=![]() ,
, ![]()
异面直线A1D1与MN的公共法向量![]() =(0,0,2),
=(0,0,2),
∴MN与A1D1的距离![]() , ∴直线MN不是“A1D1、AB的等距线”;
, ∴直线MN不是“A1D1、AB的等距线”;
异面直线A1D1与G的公共法向量![]() ,
,
∴EG与A1D1的距离d1=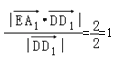 ,
,
异面直线AB与G的公共法向量![]()
∴EG与EA的距离d2= ,
,
∴EG是“A1D1、AB的等距线”;
同理,FH是“A1D1、AB的等距线”;B1D不是“A1D1、AB的等距线”.
故选:B.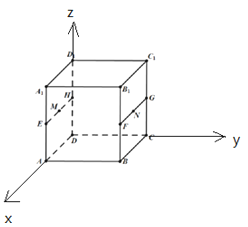

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目