题目内容
【题目】已知圆x2+y2-4ax+2ay+20a-20=0.
(1)求证:对任意实数a,该圆恒过一定点;
(2)若该圆与圆x2+y2=4相切,求a的值.
【答案】(1)见解析(2) a=1±![]() .
.
【解析】试题分析:(1)将![]() 分离,可得(x2+y2-20)+a(-4x+2y+20)=0,对任意实数
分离,可得(x2+y2-20)+a(-4x+2y+20)=0,对任意实数![]() 成立,则
成立,则![]() ,即可求出定点坐标;(2)将圆的方程化为标准方程,由题意可将两圆关系分为外切和内切,分别求出
,即可求出定点坐标;(2)将圆的方程化为标准方程,由题意可将两圆关系分为外切和内切,分别求出![]() 的值.
的值.
试题解析:(1)证明:圆的方程可整理为(x2+y2-20)+a(-4x+2y+20)=0,
此方程表示过圆x2+y2-20=0和直线-4x+2y+20=0交点的圆系.
由![]() 得
得![]()
∴已知圆恒过定点(4,-2).
(2)圆的方程可化为(x-2a)2+(y+a)2=5(a-2)2.
①当两圆外切时,d=r1+r2,
即![]() ,
,
解得a=![]() 或a=
或a=![]() (舍去);
(舍去);
②当两圆内切时,d=|r1-r2|,
即![]() ,
,
解得a=![]() 或a=
或a=![]() (舍去).
(舍去).
综上所述,a=![]() .
.

练习册系列答案
相关题目
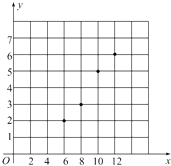
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
画出上表数据的散点图如图所示
(其中  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
(2)试根据(1)求出的线性回归方程,预测记忆力为9的学生的判断力
