题目内容
已知f(x)=xln x,g(x)=x3+ax2-x+2.
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)对一切的x∈(0,+∞),2f(x)<g′(x)+2恒成立,求实数a的取值范围.
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)对一切的x∈(0,+∞),2f(x)<g′(x)+2恒成立,求实数a的取值范围.
(1)f(x)的递减区间是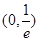 ,递增区间为
,递增区间为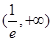 (2)f(x)min=
(2)f(x)min=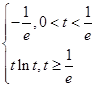 (3)[-2,+∞)
(3)[-2,+∞)
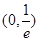 ,递增区间为
,递增区间为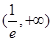 (2)f(x)min=
(2)f(x)min=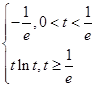 (3)[-2,+∞)
(3)[-2,+∞)(1)f(x)的定义域为(0,+∞),
f′(x)=ln x+1,
令f′(x)<0,得0<x<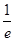 ;
;
令f′(x)>0,得x>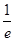 .
.
∴f(x)的递减区间是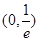 ,递增区间为
,递增区间为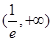 .
.
(2)(ⅰ)当0<t<t+2<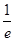 时,无解.
时,无解.
(ⅱ)当0<t<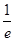 <t+2,即0<t<
<t+2,即0<t<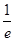 ,
,
由(1)知,f(x)min=f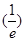 =-
=-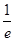 .
.
(ⅲ)当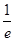 ≤t<t+2,即t≥
≤t<t+2,即t≥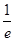 时,
时,
f(x)在区间[t,t+2]上递增,f(x)min=f(t)=tln t.
因此f(x)min=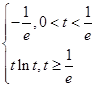
(3)2f(x)<g′(x)+2,得2xln x≤3x2+2ax+1.
∵x>0,∴a≥ln x-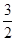 x-
x-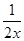 .设h(x)=ln x-
.设h(x)=ln x-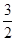 x-
x-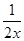 ,
,
则h′(x)=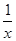 -
-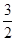 +
+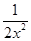 =-
=-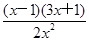 .?
.?
令h′(x)=0,得x=1,x=-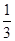 (舍).
(舍).
当0<x<1时,h′(x)>0,h(x)在(0,1)上单调递增;
当x>1时,h′(x)<0,h(x)在(1,+∞)上单调递减.
∴当x=1时,h(x)取得最大值h(x)max=-2.
∴a≥-2.
∴a的取值范围是[-2,+∞).
f′(x)=ln x+1,
令f′(x)<0,得0<x<
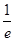 ;
;令f′(x)>0,得x>
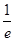 .
.∴f(x)的递减区间是
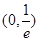 ,递增区间为
,递增区间为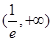 .
.(2)(ⅰ)当0<t<t+2<
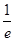 时,无解.
时,无解.(ⅱ)当0<t<
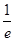 <t+2,即0<t<
<t+2,即0<t<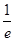 ,
,由(1)知,f(x)min=f
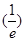 =-
=-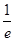 .
.(ⅲ)当
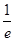 ≤t<t+2,即t≥
≤t<t+2,即t≥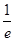 时,
时,f(x)在区间[t,t+2]上递增,f(x)min=f(t)=tln t.
因此f(x)min=
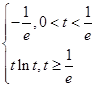
(3)2f(x)<g′(x)+2,得2xln x≤3x2+2ax+1.
∵x>0,∴a≥ln x-
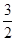 x-
x-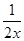 .设h(x)=ln x-
.设h(x)=ln x-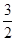 x-
x-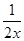 ,
,则h′(x)=
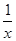 -
-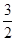 +
+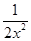 =-
=-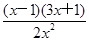 .?
.?令h′(x)=0,得x=1,x=-
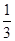 (舍).
(舍).当0<x<1时,h′(x)>0,h(x)在(0,1)上单调递增;
当x>1时,h′(x)<0,h(x)在(1,+∞)上单调递减.
∴当x=1时,h(x)取得最大值h(x)max=-2.
∴a≥-2.
∴a的取值范围是[-2,+∞).

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
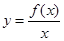 在
在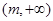 上为增函数(
上为增函数( 为常数),则称
为常数),则称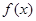 为区间
为区间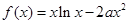 是
是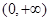 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数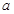 的取值范围;
的取值范围;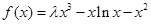 (
(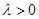 ,
,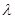 为常数),且
为常数),且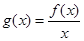 有唯一的零点,求
有唯一的零点,求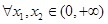 ,
,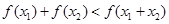
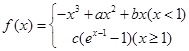 在
在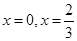 处存在极值.
处存在极值.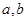 的值;
的值;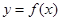 的图像上存在两点A,B使得
的图像上存在两点A,B使得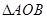 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在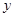 轴上,求实数
轴上,求实数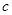 的取值范围;
的取值范围;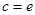 时,讨论关于
时,讨论关于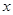 的方程
的方程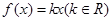 的实根个数.
的实根个数.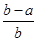 <ln
<ln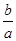 <
<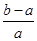 ,其中0<a<b;
,其中0<a<b;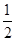 + +
+ +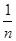 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).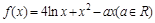 .
.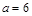 时,求函数
时,求函数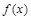 的单调区间;
的单调区间;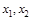 ,且
,且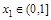 ,求证:
,求证: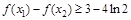 ;
;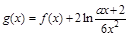 ,对于任意
,对于任意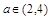 时,总存在
时,总存在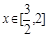 ,使
,使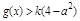 成立,求实数
成立,求实数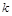 的取值范围.
的取值范围.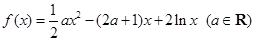 .
.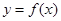 在
在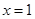 和
和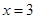 处的切线互相平行,求
处的切线互相平行,求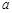 的值;
的值;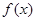 的单调区间;
的单调区间;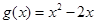 ,若对任意
,若对任意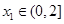 ,均存在
,均存在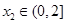 ,使得
,使得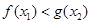 ,求
,求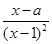 ,x∈(1,+∞).
,x∈(1,+∞).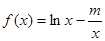 (
(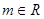 )在区间
)在区间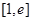 上取得最小值4,则
上取得最小值4,则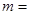 _ __.
_ __.