题目内容
已知函数f(x)=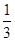 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=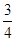 x2-bx+
x2-bx+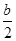 -
- ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
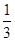 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.(1)求a,c,d的值;
(2)若h(x)=
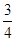 x2-bx+
x2-bx+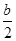 -
- ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.(1)a= ,c=
,c= d=0(2)当b>
d=0(2)当b> 时,解集为
时,解集为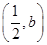 ,当b<
,当b< 时,解集为
时,解集为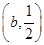 ,当b=
,当b= 时,解集为∅
时,解集为∅
 ,c=
,c= d=0(2)当b>
d=0(2)当b> 时,解集为
时,解集为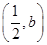 ,当b<
,当b< 时,解集为
时,解集为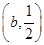 ,当b=
,当b= 时,解集为∅
时,解集为∅(1)∵f(0)=0,∴d=0,∵f′(x)=ax2- x+c.又f′(1)=0,∴a+c=
x+c.又f′(1)=0,∴a+c= .∵f′(x)≥0在R上恒成立,即ax2-
.∵f′(x)≥0在R上恒成立,即ax2- x+c≥0恒成立,∴ax2-
x+c≥0恒成立,∴ax2- x+
x+ -a≥0恒成立,显然当a=0时,上式不恒成立.∴a≠0,
-a≥0恒成立,显然当a=0时,上式不恒成立.∴a≠0,
∴
即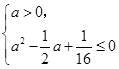 解得a=
解得a= ,c=
,c= .
.
(2)由(1)知f′(x)= x2-
x2- x+
x+ .
.
由f′(x)+h(x)<0,得 x2-
x2- x+
x+ +
+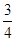 x2-bx+
x2-bx+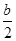 -
- <0,即x2-
<0,即x2-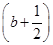 x+
x+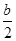 <0,
<0,
即(x-b)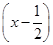 <0,当b>
<0,当b> 时,解集为
时,解集为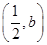 ,
,
当b< 时,解集为
时,解集为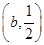 ,当b=
,当b= 时,解集为∅
时,解集为∅
 x+c.又f′(1)=0,∴a+c=
x+c.又f′(1)=0,∴a+c= .∵f′(x)≥0在R上恒成立,即ax2-
.∵f′(x)≥0在R上恒成立,即ax2- x+c≥0恒成立,∴ax2-
x+c≥0恒成立,∴ax2- x+
x+ -a≥0恒成立,显然当a=0时,上式不恒成立.∴a≠0,
-a≥0恒成立,显然当a=0时,上式不恒成立.∴a≠0,∴

即
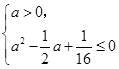 解得a=
解得a= ,c=
,c= .
.(2)由(1)知f′(x)=
 x2-
x2- x+
x+ .
.由f′(x)+h(x)<0,得
 x2-
x2- x+
x+ +
+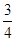 x2-bx+
x2-bx+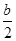 -
- <0,即x2-
<0,即x2-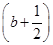 x+
x+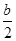 <0,
<0,即(x-b)
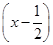 <0,当b>
<0,当b> 时,解集为
时,解集为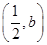 ,
,当b<
 时,解集为
时,解集为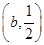 ,当b=
,当b= 时,解集为∅
时,解集为∅
练习册系列答案
相关题目
 +
+ 是否有实数解,并说明理由.
是否有实数解,并说明理由.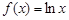 ,
,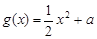 (
(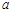 为常数),直线
为常数),直线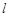 与函数
与函数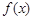 、
、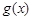 的图象都相切,且
的图象都相切,且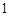 .
.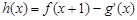 [注:
[注: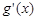 是
是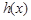 的单调递增区间;
的单调递增区间;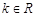 时,试讨论方程
时,试讨论方程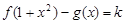 的解的个数.
的解的个数.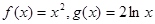 .
.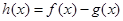 ,求
,求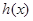 的最小值;
的最小值;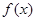 的图象,使得
的图象,使得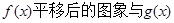 的图象有公共点且在公共点处切线相同.
的图象有公共点且在公共点处切线相同.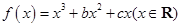 ,若
,若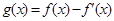 是奇函数,则
是奇函数,则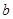 +
+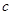 的值为
的值为 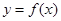 的导数
的导数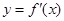 的图像,下列四个结论:
的图像,下列四个结论: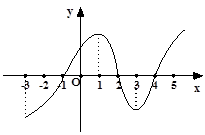
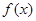 在区间
在区间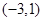 上是增函数;
上是增函数; 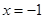 是
是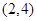 上是减函数,在区间
上是减函数,在区间 上是增函数;
上是增函数;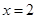 是
是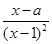 ,x∈(1,+∞).
,x∈(1,+∞).