题目内容
【题目】在直角坐标系xOy中,曲线![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为![]() .
.
(1)求C的极坐标方程和曲线M的直角坐标方程;
(2)若M与C只有1个公共点P,求m的值与P的极坐标(![]() ,
,![]() ).
).
【答案】(1)C的极坐标方程:![]() ,M的直角坐标方程:
,M的直角坐标方程:![]() ;(2)
;(2)![]() ,P的极坐标
,P的极坐标![]() .
.
【解析】
(1)由公式![]() 可进行极坐标方程与直角坐标方程的互化;
可进行极坐标方程与直角坐标方程的互化;
(2)由于圆![]() 的圆心
的圆心![]() 在圆
在圆![]() 上,因此两圆内切,从而可得
上,因此两圆内切,从而可得![]() 值,求出两圆交点坐标后再化为极坐标.
值,求出两圆交点坐标后再化为极坐标.
(1)![]() 可化为
可化为![]() ,
,
则C的极坐标方程为![]() ,
,
即![]() . M的直角坐标方程为
. M的直角坐标方程为![]() .
.
(2)易知曲线C表示经过原点圆心为![]() ,半径为2的圆,曲线M表示圆心为原点,半径为m的圆.因为M与C只有1个公共点P,所以M与C内切,
,半径为2的圆,曲线M表示圆心为原点,半径为m的圆.因为M与C只有1个公共点P,所以M与C内切,
所以![]() ,即
,即![]() . 由
. 由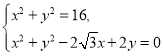 ,得
,得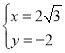 .
.
故P的极坐标![]() .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目