题目内容
设函数f (x)=cos(2x+ )+
)+ sin2x+2a
sin2x+2a
(1)求函数f (x)的单调递增区间
(2)当0≤x≤ 时,f (x)的最小值为0,求a的值.
时,f (x)的最小值为0,求a的值.
(1)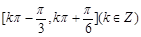 ,(2)a=-
,(2)a=- .
.
解析试题分析:(1)研究三角函数性质首先化为基本三角函数形式.即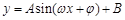 . f (x)=
. f (x)= cos2x+
cos2x+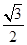 sin2x+2a=sin(2x+
sin2x+2a=sin(2x+ )+2a.再根据基本三角函数性质列不等关系:由
)+2a.再根据基本三角函数性质列不等关系:由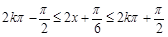 得f (x)的单调递增区间为
得f (x)的单调递增区间为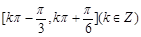 (2)由0≤x≤
(2)由0≤x≤ ,得
,得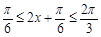 ,故
,故 ≤sin(2x+
≤sin(2x+ )≤1.由f (x)的最小值为0,得
)≤1.由f (x)的最小值为0,得 +2a=0.解得a=-
+2a=0.解得a=- .
.
解:(1)f (x)= cos2x+
cos2x+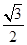 sin2x+2a=sin(2x+
sin2x+2a=sin(2x+ )+2a.
)+2a.
由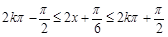 ,得kp-
,得kp- ≤x≤kp+
≤x≤kp+ (k∈Z).
(k∈Z).
所以,f (x)的单调递增区间为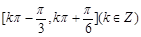 .
.
(2)由0≤x≤ ,得
,得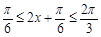 ,故
,故 ≤sin(2x+
≤sin(2x+ )≤1.
)≤1.
由f (x)的最小值为0,得 +2a=0.解得a=-
+2a=0.解得a=- .
.
考点:三角函数性质

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
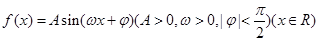 的部分图象如图所示.
的部分图象如图所示.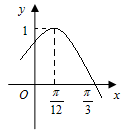
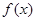 的表达式;
的表达式;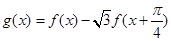 ,求函数
,求函数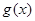 的最小值及相应的
的最小值及相应的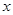 的取值集合.
的取值集合.
 的最小正周期;
的最小正周期; 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。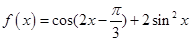 ,
,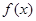 的最大值和最小正周期;
的最大值和最小正周期; 为锐角,且
为锐角,且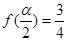 ,求
,求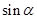 的值.
的值.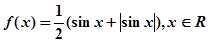
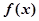 的周期T,与单调增区间.
的周期T,与单调增区间.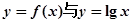 的图象有几个公共交点.
的图象有几个公共交点.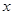 的函数
的函数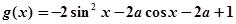 的最小值为
的最小值为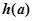 ,试确定满足
,试确定满足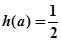 的
的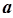 的值,并对此时的
的值,并对此时的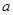 值求
值求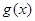 的最小值.
的最小值.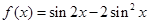
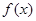 的最小正周期。
的最小正周期。 的终边经过点
的终边经过点 ,且
,且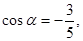
 的值.(2)求
的值.(2)求 与
与 的值.
的值. ,
, .
. 的最小正周期;
的最小正周期; 、
、 ,
, ,
, ,求
,求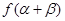 的值.
的值.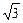 cosωx),其中0<ω<2,函数
cosωx),其中0<ω<2,函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 。
。 ,b=1,
,b=1,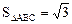 ,求a的值。
,求a的值。