题目内容
已知:函数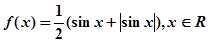
(1)求函数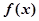 的周期T,与单调增区间.
的周期T,与单调增区间.
(2)函数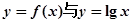 的图象有几个公共交点.
的图象有几个公共交点.
(3)设关于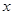 的函数
的函数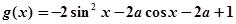 的最小值为
的最小值为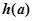 ,试确定满足
,试确定满足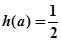 的
的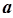 的值,并对此时的
的值,并对此时的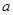 值求
值求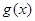 的最小值.
的最小值.
(1)函数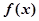 的周期为
的周期为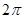 ,单调增区间为
,单调增区间为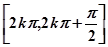 .
.
(2)函数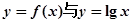 的图象有3个公共交点.
的图象有3个公共交点.
(3)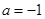 ,此时
,此时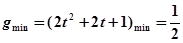 .
.
解析试题分析:(1)分类讨论去掉绝对值,即可求函数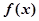 的周期T与单调增区间.(2)分别画出函数
的周期T与单调增区间.(2)分别画出函数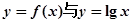 的图象,由图知有3个公共交点.(3)由题知:
的图象,由图知有3个公共交点.(3)由题知: 令
令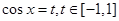 ,把
,把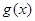 看成关于
看成关于 的二次函数,分情况讨论即可.
的二次函数,分情况讨论即可.
1)T=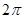 .......1分 增区间:
.......1分 增区间: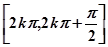 .........3分
.........3分
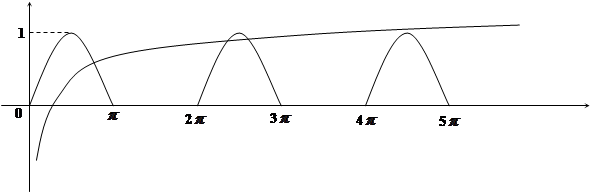
(2)作函数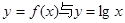 的图象,从图象可以看出函数
的图象,从图象可以看出函数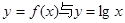 的图象有三个交点..................6分
的图象有三个交点..................6分
3)解:整理得: 令
令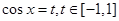 ,
,
则 ,对称轴
,对称轴 ,
,
当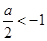 ,即
,即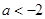 时,
时, 是函数g(x)的递增区间,
是函数g(x)的递增区间,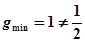 ;
;
当 ,即
,即 时,
时, 是函数
是函数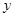 的递减区间,
的递减区间,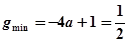
得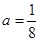 ,与
,与 矛盾;
矛盾;
当 ,即
,即 时,
时, ,得
,得 或
或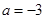 ,
,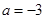 舍
舍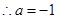 ,此时
,此时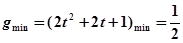 ...........12分
...........12分
考点:三角函数的图象和性质、分类讨论思想.

练习册系列答案
相关题目
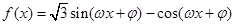 (
(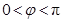 ,
,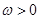 )为偶函数,且函数
)为偶函数,且函数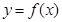 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为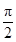 .
.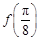 的值;
的值;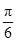 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数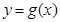 的图象,求
的图象,求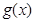 的单调递减区间.
的单调递减区间.
 ,
, .
. 中,
中,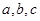 是角
是角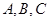 对应的边,向量
对应的边,向量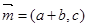 ,
,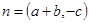 ,且
,且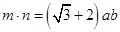 .
.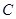 ;
;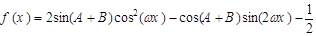 的相邻两个极值的横坐标分别为
的相邻两个极值的横坐标分别为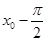 、
、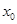 ,求
,求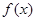 的单调递减区间.
的单调递减区间. )+
)+ sin2x+2a
sin2x+2a 时,f (x)的最小值为0,求a的值.
时,f (x)的最小值为0,求a的值.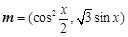 ,
,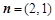 ,函数
,函数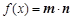 .
.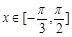 时,求函数
时,求函数 的取值范围;
的取值范围;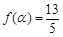 ,且
,且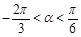 时,求
时,求 的值.
的值. ,
, .
. 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值. 的单调递增区间.
的单调递增区间. .
. 取得最大值时,求自变量
取得最大值时,求自变量 的集合;
的集合; .
. 的最小正周期和值域;
的最小正周期和值域; 中,角
中,角 的对边分别为
的对边分别为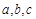 ,若
,若 且
且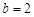 ,
,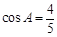 ,求
,求 和
和 .
.