题目内容
【题目】已知函数![]() 与
与![]() 的图象在点
的图象在点![]() 处有相同的切线.
处有相同的切线.
(Ⅰ)若函数![]() 与
与![]() 的图象有两个交点,求实数
的图象有两个交点,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
试题分析: (1)求出![]() 的导数,由题意可得
的导数,由题意可得 ![]() ,求出
,求出![]() ,得到
,得到![]() ,设
,设![]() ,求出导数,单调区间和最值,由题意可得只要最大值大于0,即可得到所求
,求出导数,单调区间和最值,由题意可得只要最大值大于0,即可得到所求![]() 的范围; (2)求出
的范围; (2)求出![]() 的解析式,求得导数,令
的解析式,求得导数,令![]() ,求得导数,判断
,求得导数,判断![]() ,即有
,即有![]() 在
在![]() 递增,运用分析法证明,要证
递增,运用分析法证明,要证![]() ,即证
,即证![]() ,即
,即![]() ,变形为
,变形为![]() .令
.令![]() ,即证
,即证![]() ,设
,设![]() ,求出导数,判断单调性,即可得证.
,求出导数,判断单调性,即可得证.
试题解析:
(Ⅰ)因为![]() ,
,![]() ,根据题意,得
,根据题意,得![]() 解得
解得![]()
所以![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() ,
,
又因为![]() →
→![]() 时,
时,![]() →
→![]() ;当
;当![]() →
→![]() 时,
时,![]() →
→![]() ,
,
故欲使两图象有两个交点,只需![]() ,
,![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)由![]() ,
,![]() ,得
,得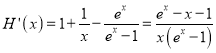 .
.
设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
要证![]() ,只需证
,只需证![]() ,即
,即![]() ,
,
变形得![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,
,
令![]() (
(![]() ),则只需证
),则只需证![]() ,设
,设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以![]() 对
对![]() 恒成立,即
恒成立,即![]() .
.

 口算题天天练系列答案
口算题天天练系列答案【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动.
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)若乙公园中每位幸运之星对每个问题答对的概率均为![]() ,求恰好2位幸运之星获得纪念品的概率;
,求恰好2位幸运之星获得纪念品的概率;
(Ⅲ)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: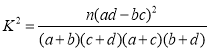
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |