题目内容
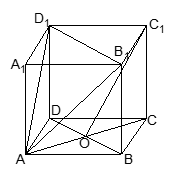
(本题满分15分)已知正方体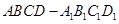 的棱长为1,点
的棱长为1,点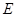 在
在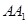 上,点
上,点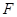 在
在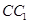 上,且
上,且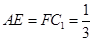
(1)求直线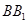 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(2)用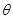 表示平面
表示平面 和侧面
和侧面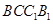 所成的锐二面角的大小,求
所成的锐二面角的大小,求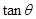 ;
;
(3)若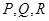 分别在
分别在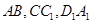 上,并满足
上,并满足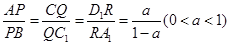 ,探索:当
,探索:当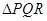 的重心为
的重心为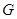 且
且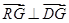 时,求实数
时,求实数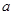 的取值范围.
的取值范围.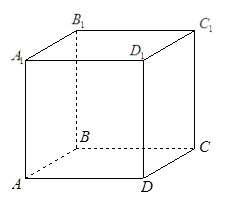
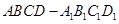 的棱长为1,点
的棱长为1,点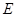 在
在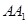 上,点
上,点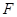 在
在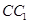 上,且
上,且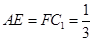
(1)求直线
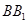 与平面
与平面 所成角的余弦值;
所成角的余弦值;(2)用
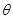 表示平面
表示平面 和侧面
和侧面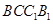 所成的锐二面角的大小,求
所成的锐二面角的大小,求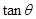 ;
;(3)若
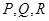 分别在
分别在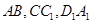 上,并满足
上,并满足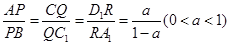 ,探索:当
,探索:当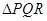 的重心为
的重心为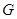 且
且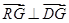 时,求实数
时,求实数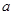 的取值范围.
的取值范围.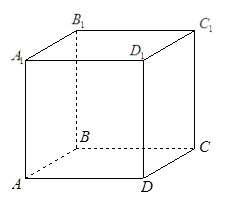
(1)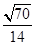 (2)
(2) ,则
,则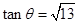 (3)
(3)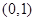 .
.
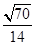 (2)
(2) ,则
,则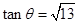 (3)
(3)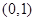 .
. 第一问中利用以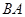 为
为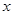 轴,
轴,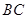 为
为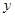 轴,
轴,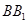 为
为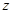 轴建立空间直角坐标系
轴建立空间直角坐标系
设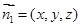 为平面
为平面 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,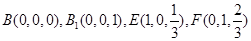
借助于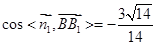 ,得到结论
,得到结论
第二问中,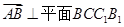 ,
,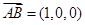 是平面
是平面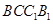 的法向量
的法向量
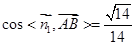 ,又平面
,又平面 和侧面
和侧面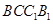 所成的锐二面角为
所成的锐二面角为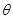
 ,则
,则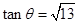
第三问中,因为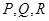 分别在
分别在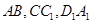 上,且
上,且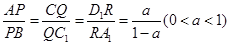
故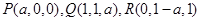 ,
,
所以当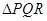 的重心为
的重心为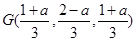
然后利用垂直关系得到结论。
解:(1)以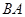 为
为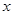 轴,
轴,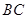 为
为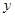 轴,
轴,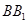 为
为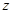 轴建立空间直角坐标系
轴建立空间直角坐标系
又正方体的棱长为1,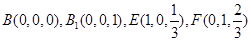
设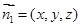 为平面
为平面 的法向量
的法向量
 令
令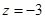 ,则
,则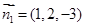
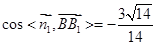
设直线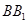 与平面
与平面 所成角为
所成角为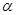 ,
,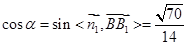
直线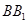 与平面
与平面 所成角的余弦值为
所成角的余弦值为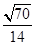 (5分)
(5分)
(2)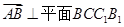 ,
,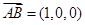 是平面
是平面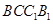 的法向量
的法向量
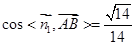 ,又平面
,又平面 和侧面
和侧面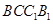 所成的锐二面角为
所成的锐二面角为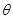
 ,则
,则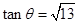 (5分)
(5分)
(3)因为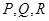 分别在
分别在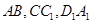 上,且
上,且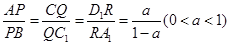
故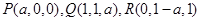 ,
,
所以当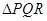 的重心为
的重心为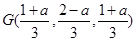 ,而
,而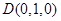
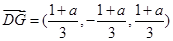 ,
,
当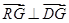 时,
时,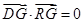
 为恒等式
为恒等式
所以,实数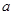 的取值范围为
的取值范围为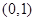 (5分)
(5分)
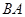 为
为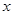 轴,
轴,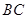 为
为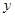 轴,
轴,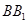 为
为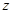 轴建立空间直角坐标系
轴建立空间直角坐标系设
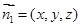 为平面
为平面 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,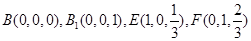
借助于
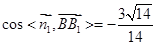 ,得到结论
,得到结论第二问中,
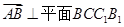 ,
,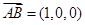 是平面
是平面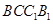 的法向量
的法向量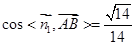 ,又平面
,又平面 和侧面
和侧面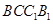 所成的锐二面角为
所成的锐二面角为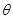
 ,则
,则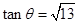
第三问中,因为
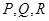 分别在
分别在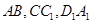 上,且
上,且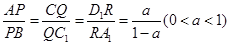
故
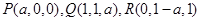 ,
,所以当
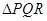 的重心为
的重心为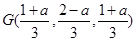
然后利用垂直关系得到结论。
解:(1)以
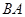 为
为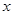 轴,
轴,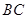 为
为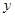 轴,
轴,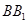 为
为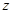 轴建立空间直角坐标系
轴建立空间直角坐标系又正方体的棱长为1,
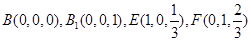
设
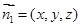 为平面
为平面 的法向量
的法向量 令
令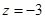 ,则
,则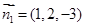
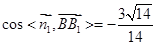
设直线
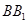 与平面
与平面 所成角为
所成角为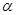 ,
,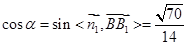
直线
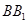 与平面
与平面 所成角的余弦值为
所成角的余弦值为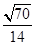 (5分)
(5分)(2)
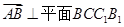 ,
,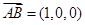 是平面
是平面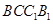 的法向量
的法向量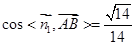 ,又平面
,又平面 和侧面
和侧面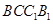 所成的锐二面角为
所成的锐二面角为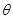
 ,则
,则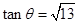 (5分)
(5分)(3)因为
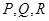 分别在
分别在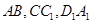 上,且
上,且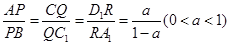
故
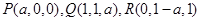 ,
,所以当
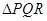 的重心为
的重心为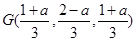 ,而
,而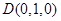
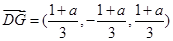 ,
,
当
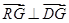 时,
时,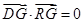
 为恒等式
为恒等式所以,实数
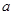 的取值范围为
的取值范围为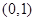 (5分)
(5分)
练习册系列答案
相关题目
 ,
, 是垂足.
是垂足.
 平面
平面 ;
;  ,求证:
,求证:

 .
.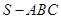 中,各个面都是边长为
中,各个面都是边长为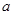 的正三角形,
的正三角形,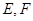 分别是
分别是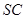 和
和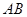 的中 点,则异面直线
的中 点,则异面直线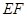 与
与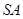 所成的角等于( )
所成的角等于( )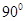 B
B 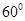 C
C 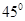 D
D 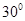
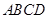 ,
,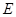 是
是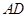 中点,则直线
中点,则直线 与直线
与直线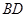 所成的角的余弦值为( )
所成的角的余弦值为( ) 




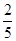


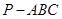 中,
中,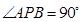 ,
,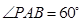 ,
,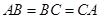 ,平面
,平面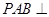 平面
平面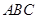 。
。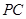 与平面
与平面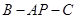 的大小。
的大小。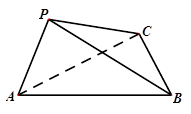
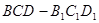 与四棱锥
与四棱锥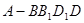 的组合体中,已知
的组合体中,已知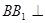 平面
平面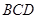 ,四边形
,四边形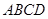 是平行四边形,
是平行四边形,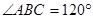 ,
,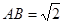 ,
,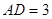 ,
,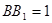 。
。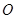 是线段
是线段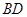 的中点,求证:
的中点,求证: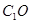 ∥平面
∥平面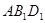 ;
;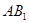 与平面
与平面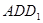 所成的角。
所成的角。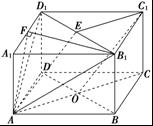
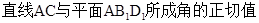 .
.
 中,下列结论正确的是( ).
中,下列结论正确的是( ).



