题目内容
【题目】如图,三棱台![]() 中, 侧面
中, 侧面![]() 与侧面
与侧面![]() 是全等的梯形,若
是全等的梯形,若![]() ,且
,且![]() .
.

(Ⅰ)若![]() ,
, ![]() ,证明:
,证明: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若二面角![]() 为
为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ) 连接![]() ,由比例可得
,由比例可得![]() ∥
∥![]() ,进而得线面平行;
,进而得线面平行;
(Ⅱ)过点![]() 作
作![]() 的垂线,建立空间直角坐标系,不妨设
的垂线,建立空间直角坐标系,不妨设![]() ,则
,则![]() 求得平面
求得平面![]() 的法向量为
的法向量为![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 求二面角余弦即可.
求二面角余弦即可.
试题解析:
(Ⅰ)证明:连接![]() ,梯形
,梯形![]() ,
, ![]() ,
,
易知: ![]() ;
;
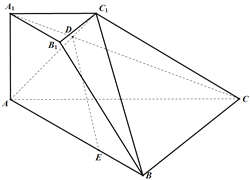
又![]() ,则
,则![]() ∥
∥![]() ;
;
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
可得: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)侧面![]() 是梯形,
是梯形, ![]() ,
,
![]() ,
, ![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角,
的平面角, ![]()
![]() ;
;
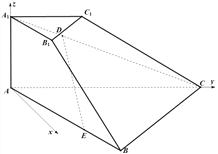
![]() 均为正三角形,在平面
均为正三角形,在平面![]() 内,过点
内,过点![]() 作
作![]() 的垂线,如图建立空间直角坐标系,不妨设
的垂线,如图建立空间直角坐标系,不妨设![]() ,则
,则![]()
![]() ,故点
,故点![]() ,
, ![]()
![]() ;
;
设平面![]() 的法向量为
的法向量为![]() ,则有:
,则有: 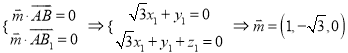 ;
;
设平面![]() 的法向量为
的法向量为![]() ,则有:
,则有: 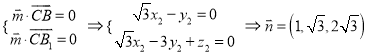 ;
;
![]() ,
,
故平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】已知函数![]() ,正实数a,b,c是公差为正数的等差数列,且满足
,正实数a,b,c是公差为正数的等差数列,且满足![]() .若实数d是方程
.若实数d是方程![]() 的一个解,那么下列三个判断:①d<a;②d<b;③d<c中有可能成立的个数为( )
的一个解,那么下列三个判断:①d<a;②d<b;③d<c中有可能成立的个数为( )
A. 0 B. 1 C. 2 D. 3
【题目】在某中学高中某学科竞赛中,该中学100名考生的参赛成绩统计如图所示.

(1)求这100名考生的竞赛平均成绩(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 18 | ||
女生 | 25 | ||
合计 | 100 |
附:![]() .
.
| 0.050 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
