题目内容
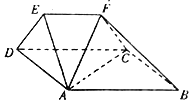
【题目】如图,已知梯形![]() 与梯形
与梯形![]() 全等,
全等, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.

(Ⅰ)证明: ![]() 平面
平面![]()
(Ⅱ)点![]() 在线段
在线段![]() 上(端点除外),且
上(端点除外),且![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ):设![]() 为
为![]() 中点,连结
中点,连结![]() ,易得四边形
,易得四边形![]() 是平行四边形,有
是平行四边形,有![]() ,进而可证线面平行;
,进而可证线面平行;
(Ⅱ)由![]() ,
, ![]() 得
得![]() 平面
平面![]() ,以
,以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 的方向分别为
的方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() .设点
.设点![]() 在
在![]() 上,且
上,且![]() ,求得平面
,求得平面![]() 的个法向量
的个法向量![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() ,从而得解.
,从而得解.
试题解析:
(Ⅰ)证明:方法一:设![]() 为
为![]() 中点,连结
中点,连结![]() ,因为
,因为![]() 为
为![]() 中点,
中点,
所以![]() 是
是![]() 的中位线,
的中位线, ![]() .
.
由已知![]() ,所以
,所以![]() ,因此四边形
,因此四边形![]() 是平行四边形,
是平行四边形,
所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
方法二:延长线段![]() ,
, ![]() ,交于点
,交于点![]() ,连结
,连结![]() ,由
,由![]() ,则
,则![]() 是
是![]() 的中点,又
的中点,又![]() 是
是![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,所以
的中位线,所以![]() .
.
又![]() 平由
平由![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)由梯形![]() 与梯形
与梯形![]() 全等,
全等,
因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() .
.
![]() 中,
中, ![]() ,
, ![]()
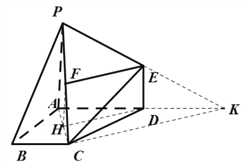
所以![]() .因为
.因为![]() ,
,
故有![]() ,从而
,从而![]() ,
,
又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 的方向分别为
的方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() .设点
.设点![]() 在
在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,所以
,所以![]() ,
, ![]()
设![]() 是平面
是平面![]() 的个法向量,则
的个法向量,则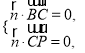
即![]() 取
取![]()
![]() ,
,
故![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() ,即
,即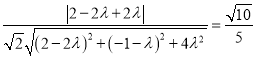 .
.
解得![]() ,
, ![]() (舍去),故
(舍去),故![]() .
.

练习册系列答案
相关题目
【题目】某市电力公司为了制定节电方案,需要了解居民用电情况,通过随机抽样,电力公司获得了![]() 户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).
户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求![]() ,
, ![]() 的值;
的值;
(2)为了解用电量较大的用户用电情况,在第![]() 、
、![]() 两组用分层抽样的方法选取
两组用分层抽样的方法选取![]() 户.
户.
①求第![]() 、
、![]() 两组各取多少户?
两组各取多少户?
②若再从这![]() 户中随机选出
户中随机选出![]() 户进行入户了解用电情况,求这
户进行入户了解用电情况,求这![]() 户中至少有一户月平均用电量在
户中至少有一户月平均用电量在![]() 范围内的概率.
范围内的概率.