题目内容
如图,已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C.

(1)求侧面A1ABB1与底面ABC所成二面角的大小;
(2)求顶点C到侧面A1ABB1的距离;
(3)求异面直线A1C与BC1所成的角.
答案:
解析:
解析:
|
(1)取AC中点D连A1D,则易知A1D ∵A1D= (2)设C到侧面A1ABB1的距离为h,∴ 又∵ 即顶点C到侧面A1ABB1的距离为 (3)取 ∴ ∴异面直线 |

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
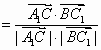
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=