题目内容
.函数f(x)=
.给出函数f(x)下列性质:(1)f(x)的定义域和值域均为[-1,1];(2)f(x)是奇函数;(3)函数在定义域上单调递增;(4)函数f(x)有两零点;(5)A、B为函数f(x)图象上任意不同两点,则
<|AB|≤2.则函数f(x)有关性质中正确描述的个数是( )
| ||
| |x-2|-2 |
| 2 |
| A.1 | B.2 | C.3 | D.4 |
∵
∴函数定义域为
-1≤x<0或0<x≤1,}
∴f(x)=
=
=
作出函数图象,如图所示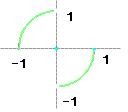
由图象可知函数定义域为[-1,0)∪(0,1],值域为(-1,1)故(1)不正确;
∵函数定义域关于原点对称且
f(-x)=
=
=-f(x)
∴函数f(x)为奇函数,故(2)正确;
由图象可知函数在[-1,0)上为单调增函数,在(0,1]上也是单调增函数,但在定义域上不是增函数,如-1<1,但f(-1)>f(1).故(3)不正确;
由图象可知函数的零点为x=-1,x=1,故(4)正确;
由图象可知图象为两个四分之一个圆弧构成,且半径为1,最大为AB连线过原点时最大为2,最小为
,但取不到.
故(5)正确.
故选C.
|
|
∴f(x)=
| ||
| -(x-2)-2 |
|x|
| ||
| -x |
|
作出函数图象,如图所示

由图象可知函数定义域为[-1,0)∪(0,1],值域为(-1,1)故(1)不正确;
∵函数定义域关于原点对称且
f(-x)=
|-x|
| ||
| -(-x) |
|x|
| ||
| x |
∴函数f(x)为奇函数,故(2)正确;
由图象可知函数在[-1,0)上为单调增函数,在(0,1]上也是单调增函数,但在定义域上不是增函数,如-1<1,但f(-1)>f(1).故(3)不正确;
由图象可知函数的零点为x=-1,x=1,故(4)正确;
由图象可知图象为两个四分之一个圆弧构成,且半径为1,最大为AB连线过原点时最大为2,最小为
| 2 |
故(5)正确.
故选C.

练习册系列答案
相关题目