题目内容
已知定义域为R的函数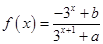 是奇函数.
是奇函数.
(1)求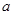 ,
,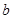 的值;
的值;
(2)证明函数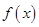 的单调性.
的单调性.
(1) ,
,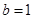 ;(2)见解析.
;(2)见解析.
解析试题分析:(1)因为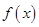 是定义在R上的奇函数,所以有
是定义在R上的奇函数,所以有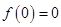 ,解得
,解得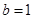 ,再由
,再由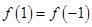 ,解得
,解得 ;(2)根据单调递减函数的定义证明:先由(1)写出函数
;(2)根据单调递减函数的定义证明:先由(1)写出函数 的解析式,
的解析式,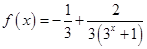 ,然后取任意的
,然后取任意的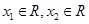 且
且 ,对
,对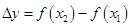 化简得到
化简得到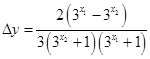 ,根据
,根据 以及指数函数的性质可以判断
以及指数函数的性质可以判断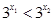 ,所以
,所以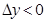 ,即
,即 时,有
时,有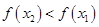 ,根据单调递减函数的定义可知,函数
,根据单调递减函数的定义可知,函数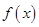 在全体实数R上是单调递减函数.
在全体实数R上是单调递减函数.
试题解析:(1)因为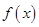 是定义在R上的奇函数,
是定义在R上的奇函数,
所以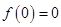 ,即
,即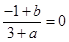 ,解得
,解得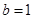 . 2分
. 2分
从而有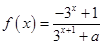 .
.
又由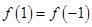 知,
知,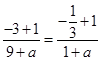 ,解得
,解得 . 5分
. 5分
(2)由(1)知 , 7分
, 7分
对于任意的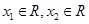 且
且 , 8分
, 8分
∵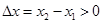 ,
,
∴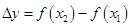

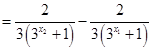
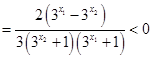 11分
11分
所以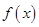 在全体实数上为单调减函数. 12分
在全体实数上为单调减函数. 12分
考点:1.奇函数的性质;2.求函数解析式;3.待定系数法;4.函数的单调性;5.指数函数的性质

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元. .
. 时,判断
时,判断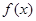 的奇偶性,并说明理由;
的奇偶性,并说明理由;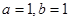 时,若
时,若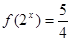 ,求
,求 的值;
的值;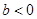 ,且对任何
,且对任何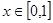 不等式
不等式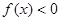 恒成立,求实数
恒成立,求实数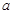 的取值范围.
的取值范围. 。
。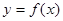 的定义域;
的定义域; 的值,作出函数
的值,作出函数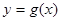 的图象并指出函数
的图象并指出函数 ,
,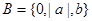 且
且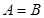 .
.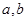 的值;
的值; 在
在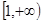 的单调性,并用定义加以证明.
的单调性,并用定义加以证明. .
. 的定义域为A,求集合A;
的定义域为A,求集合A;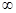 )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明.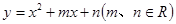 ,当
,当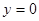 时,对应
时,对应 值的集合为
值的集合为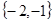 .
.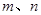 的值;(2)若
的值;(2)若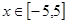 ,求该函数的最值.
,求该函数的最值.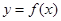 来拟合该景点对外开放的第
来拟合该景点对外开放的第
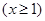 年与当年的游客人数
年与当年的游客人数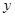 (单位:万人)之间的关系.
(单位:万人)之间的关系.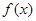 =
=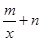 ,试确定
,试确定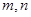 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测;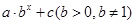 ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定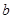 的取值范围.
的取值范围. 的定义域为
的定义域为 .
.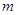 的取值范围;
的取值范围;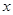 的不等式
的不等式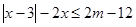 .
.