题目内容
【题目】为践行“绿水青山就是金山银山”的国家发展战略,我市对某辖区内畜牧、化工、煤炭三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到85分及其以上的单位被称为“![]() 类”环保单位,未达到85分的单位被称为“
类”环保单位,未达到85分的单位被称为“![]() 类”环保单位.现通过分层抽样的方法确定了这三类行业共20个单位进行调研,统计考评分数如下:
类”环保单位.现通过分层抽样的方法确定了这三类行业共20个单位进行调研,统计考评分数如下:
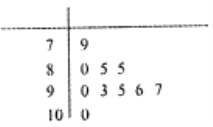
畜牧类行业:85,92,77,81,89,87
化工类行业:79,77,90,85,83,91
煤炭类行业:87,89,76,84,75,94,90,88
(1)计算该辖区这三类行业中每类行业的单位个数;
(2)若从畜牧类行业这六个单位中,再随机选取两个单位进行生产效益调查,求选出的这两个单位中既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() 类”环保单位的概率.
类”环保单位的概率.
【答案】(1)60、60、80;(2)![]()
【解析】
(1)求出三类行业的个数之比,结合分层抽样的定义可求出每类行业的单位个数.
(2)列举出六个单位中随机抽取两个所有的组合情况,即可得到总的事件个数及既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() 类”环保单位的组合个数,结合古典概型即可求概率.
类”环保单位的组合个数,结合古典概型即可求概率.
解:(1)由题意得,抽取的畜牧、化工、煤炭三类行业单位个数之比为![]() .
.
由分层抽样的定义,有畜牧类行业的单位个数为![]() ,
,
化工类行业的单位个数为![]() ,煤炭类行业的单位个数为
,煤炭类行业的单位个数为![]() ,
,
故该辖区畜牧、化工、煤炭三类行业中每类行业的单位个数分别为60、60、80.
(2)记选出的这2个单位中既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() ”环保单位为事件
”环保单位为事件![]() .这2个单位的考核数据情形有
.这2个单位的考核数据情形有
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15种.
共15种.
其中符合的事件![]() 的考核数据情形有
的考核数据情形有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8种,故所求概率
共8种,故所求概率![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】出版商为了解某科普书一个季度的销售量![]() (单位:千本)和利润
(单位:千本)和利润![]() (单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
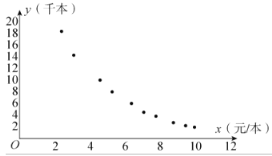
根据上述数据画出如图所示的散点图:
(1)根据图中所示的散点图判断![]() 和
和![]() 哪个更适宜作为销售量
哪个更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型?(给出判断即可,不需要说明理由)
的回归方程类型?(给出判断即可,不需要说明理由)
(2)根据(1)中的判断结果及参考数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)根据回归方程设该科普书一个季度的利润总额为![]() (单位:千元),当季销售量
(单位:千元),当季销售量![]() 为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
参考公式及参考数据:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的公式分别为
的斜率和截距的公式分别为 .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .计算时,所有的小数都精确到0.01.
.计算时,所有的小数都精确到0.01.