题目内容
给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则它们共同具有的性质是( )
| A.周期性 | B.偶函数 | C.奇函数 | D.无最大值 |
C
解析试题分析: 为奇函数且周期为
为奇函数且周期为 ;
; 为奇函数且周期为
为奇函数且周期为 ;
; 由图像可知此函数为奇函数无周期性;
由图像可知此函数为奇函数无周期性; 由图像可知此函数为奇函数无周期性。所以这些函数共同具有的性质是奇函数。
由图像可知此函数为奇函数无周期性。所以这些函数共同具有的性质是奇函数。
考点:1函数的奇偶性,周期性;2函数图像。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
方程 的解所在的区间是( )
的解所在的区间是( )
A. | B. | C. | D. |
函数 的定义域是 ( )
的定义域是 ( )
A. | B.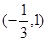 | C. | D. |
已知 是定义在
是定义在 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的 都满足
都满足 ,则
,则 是
是
| A.奇函数 | B.偶函数 |
| C.不是奇函数也不是偶函数 | D.既是奇函数又是偶函数 |
定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
在定义域内既是奇函数又为增函数的是( )
A. | B. | C. | D. |
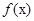 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,则当
,则当 时,
时, ( )
( )
A.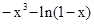 | B. | C. | D. |
 的导函数
的导函数 的图象如图所示,那么函数
的图象如图所示,那么函数
 切直线
切直线 于
于 点,射线
点,射线 从
从 出发绕着
出发绕着 ,旋转过程中
,旋转过程中 ,记
,记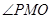 为
为 ,弓形
,弓形 的面积
的面积 ,那么
,那么 的大致图象是 ( )
的大致图象是 ( )
