题目内容
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
【答案】(1)见解析(2)1
【解析】试题分析:(1)当![]() 时,对
时,对![]() 求导,
求导, ![]() 得增区间,
得增区间,![]() 得减区间,进而求出函数的最小值值,即可证明;(2)若t>
得减区间,进而求出函数的最小值值,即可证明;(2)若t>![]() ,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
试题解析:解:(1)t=1时,f(x)=x﹣![]() ﹣2lnx,x>0
﹣2lnx,x>0
∴f′(x)=1+![]() ﹣
﹣![]() =
=![]() =
=![]() ≥0,
≥0,
∴f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1﹣1﹣0=0,
∴x>1,f(x)>0成立,
(2)当x∈(0,+∞),g(x)=tx2﹣(t+1)xlnx+(t+1)x﹣1
∴g′(x)=2tx﹣(t+1)lnx,
设m(x)=2tx﹣(t+1)lnx, ∴m′(x)=2t﹣![]() =
=![]() ,
,
令m′(x)=0,得x=![]() ,
,
当0<x<![]() 时,m'(x)<0;当时x>
时,m'(x)<0;当时x>![]() ,m'(x)>0.
,m'(x)>0.
∴g'(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴g'(x)的最小值为g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() ),
),
∵t>![]() ,∴
,∴![]() =
=![]() +
+![]() <
<![]() +
+![]() <e.
<e.
∴g'(x)的最小值g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() )>0,
)>0,
从而,g(x)在区间(0,+∞)上单调递增.
又g(1)=2t>0,又g(![]() )=
)=![]() +
+![]() (6+2lnt)﹣1,
(6+2lnt)﹣1,
设h(t)=e3t﹣(2lnt+6).
则h′(t)=e3﹣![]() .
.
令h'(t)=0得t=![]() .由h'(t)<0,得0<t<
.由h'(t)<0,得0<t<![]() ;
;
由h'(t)>0,得t>![]() .
.
∴h(t)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴h(t)min=h(![]() )=2﹣2ln2>0.
)=2﹣2ln2>0.
∴h(t)>0恒成立.∴e3t>2lnt+6,.
∴g(![]() )<
)<![]() +
+![]() ﹣1=
﹣1=![]() +
+![]() +
+![]() ﹣1<
﹣1<![]() +
+![]() +
+![]() ﹣1<0.
﹣1<0.
∴当t>![]() 时,函数g(x)恰有1个零点
时,函数g(x)恰有1个零点

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】为了增强环保意识,某社团从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市举办的环保知识竞赛,学校举办预选赛,现在环保测试优秀的同学中选3人参加预选赛,已知在环保测试中优秀的同学通过预选赛的概率为![]() ,若随机变量
,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() =
=![]()
| 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: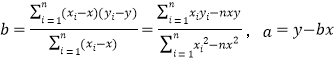 ,).
,).