题目内容
(本题满分8分)
已知经过点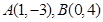 的圆
的圆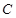 与圆
与圆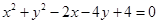 相交,它们的公共弦平行于直线
相交,它们的公共弦平行于直线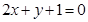 .
.
(Ⅰ)求圆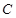 的方程;
的方程;
(Ⅱ)若动圆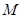 经过一定点
经过一定点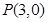 ,且与圆
,且与圆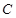 外切,求动圆圆心
外切,求动圆圆心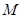 的轨迹方程.
的轨迹方程.
已知经过点
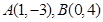 的圆
的圆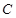 与圆
与圆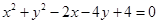 相交,它们的公共弦平行于直线
相交,它们的公共弦平行于直线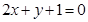 .
.(Ⅰ)求圆
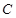 的方程;
的方程;(Ⅱ)若动圆
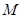 经过一定点
经过一定点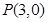 ,且与圆
,且与圆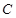 外切,求动圆圆心
外切,求动圆圆心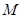 的轨迹方程.
的轨迹方程.解:(Ⅰ)设圆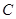 的方程为
的方程为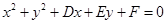 ,
,
则两圆的公共弦方程为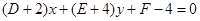 ,
,
由题意得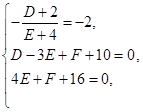
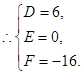
∴圆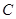 的方程为
的方程为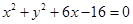 ,即
,即  .………………4分
.………………4分
(Ⅱ)圆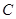 的圆心为
的圆心为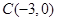 ,半径
,半径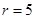 .
.
∵动圆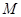 经过一定点
经过一定点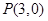 ,且与圆
,且与圆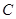 外切.
外切.
∴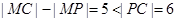 .
.
∴动圆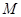 圆心的轨迹是以
圆心的轨迹是以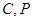 为焦点,实轴长为
为焦点,实轴长为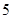 的双曲线的右支.………7分
的双曲线的右支.………7分
设双曲线的方程为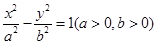 ,
,
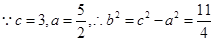 ,
,
故动圆圆心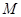 的轨迹方程是
的轨迹方程是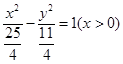 .………………8分
.………………8分
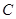 的方程为
的方程为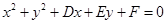 ,
,则两圆的公共弦方程为
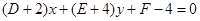 ,
, 由题意得
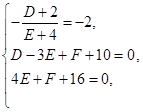
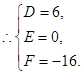
∴圆
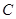 的方程为
的方程为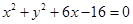 ,即
,即  .………………4分
.………………4分(Ⅱ)圆
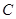 的圆心为
的圆心为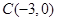 ,半径
,半径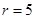 .
.∵动圆
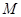 经过一定点
经过一定点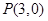 ,且与圆
,且与圆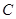 外切.
外切.∴
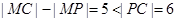 .
.∴动圆
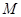 圆心的轨迹是以
圆心的轨迹是以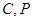 为焦点,实轴长为
为焦点,实轴长为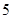 的双曲线的右支.………7分
的双曲线的右支.………7分设双曲线的方程为
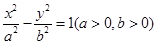 ,
,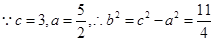 ,
,故动圆圆心
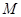 的轨迹方程是
的轨迹方程是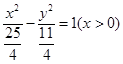 .………………8分
.………………8分略

练习册系列答案
相关题目
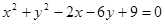 关于直线
关于直线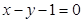 对称的圆的方程为
对称的圆的方程为


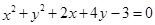 上,且到直线
上,且到直线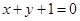 的距离为
的距离为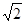 的点共有( )
的点共有( )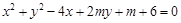 与
与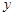 轴的两交点
轴的两交点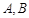 位于原点的同侧,则实数
位于原点的同侧,则实数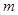

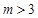 或
或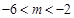
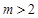 或
或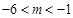
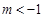
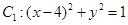 ,圆
,圆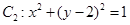 ,圆
,圆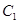 ,
,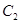 关于直线
关于直线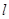 对称.
对称.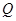 ,使
,使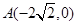 点的距离减去
点的距离减去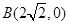 点的距离的差为
点的距离的差为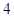 ,如果存在求出
,如果存在求出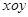 中,已知“葫芦”曲线
中,已知“葫芦”曲线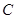 由圆弧
由圆弧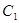 与圆弧
与圆弧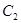 相接而成,两相接点
相接而成,两相接点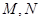 均在直线
均在直线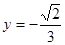 上.圆弧
上.圆弧 ,半径为
,半径为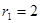 ;圆弧
;圆弧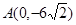 .
.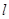 :
: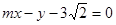 与“葫芦”曲线
与“葫芦”曲线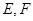 两点.当
两点.当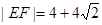 时,求直线
时,求直线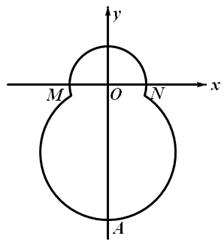
 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线 是否与直线
是否与直线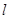 与圆
与圆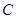 相交于点
相交于点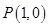 和点
和点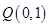 。
。