题目内容
过抛物线y2=2px(p>0)焦点F的直线与抛物线交于P、Q,由P、Q分别引其准线的垂线PH1、QH2垂足分别为H1、H2,H1H2的中点为M,记|PF|=a,|QF|=b,则|MF|=______.
①PQ与x轴不垂直时,如图所示,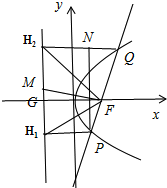
由抛物线的定义,可得|PF|=|PH1|,|QF|=|QH2|.
∴∠PFH1=∠PH1F,∠QFH2=∠QH2F,
设准线交x轴于点G,
∵QH2∥FG∥PH1,∴∠H2FG=∠QH2F,∠H1FG=∠PH1F.
因此∠H2FG=∠QFH2,且∠H1FG=∠PFH1,
可得∠H2FG+∠H1FG=
×180°=90°.
∴Rt△H1H2F中,中线|MF|=
|H1H2|.
过点P作PN⊥QS,垂足为N,则|PN|=|H1H2|.
在Rt△PQN中,|PQ|=|PH1|+|QH2|=a+b,|QN|=||PH1|-|QH2||=|a-b|,
∴|PN|=
=
=2
.可得|MF|=
|H1H2|=
.
②当PQ⊥x轴时,可得p=a=b,此时|MF|=p=
也成立.
综上所述,可得MF的长等于
故答案为:

由抛物线的定义,可得|PF|=|PH1|,|QF|=|QH2|.
∴∠PFH1=∠PH1F,∠QFH2=∠QH2F,
设准线交x轴于点G,
∵QH2∥FG∥PH1,∴∠H2FG=∠QH2F,∠H1FG=∠PH1F.
因此∠H2FG=∠QFH2,且∠H1FG=∠PFH1,
可得∠H2FG+∠H1FG=
| 1 |
| 2 |
∴Rt△H1H2F中,中线|MF|=
| 1 |
| 2 |
过点P作PN⊥QS,垂足为N,则|PN|=|H1H2|.
在Rt△PQN中,|PQ|=|PH1|+|QH2|=a+b,|QN|=||PH1|-|QH2||=|a-b|,
∴|PN|=
| |PQ|2-|QN|2 |
| (a+b)2+(a-b)2 |
| ab |
| 1 |
| 2 |
| ab |
②当PQ⊥x轴时,可得p=a=b,此时|MF|=p=
| ab |
综上所述,可得MF的长等于
| ab |
故答案为:
| ab |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目