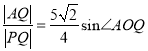题目内容
【题目】我国南宋时期著名的数学家秦九韶在其著作《数书九章》中，提出了已知三角形三边长求三角形的面积的公式，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂减上，余四约之，为实．一为从隔，开平方得积．”若把以上这段文字写成公式，即
，其中a、b、c分别为
内角A、B、C的对边.若
，
，则面积S的最大值为
A. 
B. 
C. 
D. 
【答案】C
【解析】
将已知等式进行化简并利用正弦定理可得c=
a，代入“三斜求积”公式即可计算得解．
∵
，则sinC＝（sinBcosC+cosBsinC）＝sin（B+C）＝sinA，由正弦定理得c＝a，∵b＝2，
△ABC的面积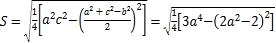
＝
，∴当
即a＝2时，△ABC的面积S有最大值为．
故选：C．
练习册系列答案
相关题目
