题目内容
【题目】设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点 |
B.存在定点P不在M中的任一条直线上 |
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上 |
D.M中的直线所能围成的正三角形面积都相等 |
其中真命题的代号是 (写出所有真命题的代号).
【答案】BC
【解析】试题分析:因为点![]() 到直线系
到直线系![]() 中每条直线的距离
中每条直线的距离![]() ,直线系
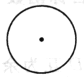
,直线系![]() 表示圆
表示圆![]() 的切线的集合.A.由于直线系表示圆
的切线的集合.A.由于直线系表示圆![]() 的所有切线,其中存在两条切线平行,
的所有切线,其中存在两条切线平行, ![]() 中所有直线均经过一个定点
中所有直线均经过一个定点![]() 不可能,故A不正确;B.存在定点
不可能,故A不正确;B.存在定点![]() 不在
不在![]() 中的任一条直线上,观察点
中的任一条直线上,观察点![]() 即符合条件,故B正确;C.由于圆的所有外切正多边形的边都是圆的切线, 所以对于任意整数
即符合条件,故B正确;C.由于圆的所有外切正多边形的边都是圆的切线, 所以对于任意整数![]() ,存在正
,存在正![]() 边形,其所有边均在
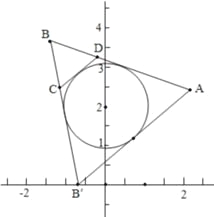
边形,其所有边均在![]() 中的直线上,故C正确;D.如图,
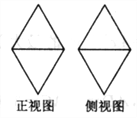
中的直线上,故C正确;D.如图, ![]() 中的直线所能围成的正三角形有两类,其一是如
中的直线所能围成的正三角形有两类,其一是如![]() 是圆的外切三角形,此类面积都相等,另一类是在圆同一侧,如
是圆的外切三角形,此类面积都相等,另一类是在圆同一侧,如![]() 型,此一类面积相等,但两类之间面积不等,所以面积大小不一定相等,故本命题不正确,故选BC.
型,此一类面积相等,但两类之间面积不等,所以面积大小不一定相等,故本命题不正确,故选BC.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目