题目内容
定义在R上的奇函数f(x),当x≥0时,f(x)= 则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
 则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ). | A.1-2a | B.2a-1 |
| C.1-2-a | D.2-a-1 |
A
当0≤x<1时,f(x)≤0,当x≥1时,函数f(x)=1-|x-3|,关于x=3对称,当x≤-1时,函数关于x=-3对称,由F(x)=f(x)-a=0(0<a<1),得y=f(x),y=a,所以函数F(x)=f(x)-a有5个零点.当-1≤x≤0时,0<-x≤1,所以f(-x)=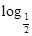 (-x+1)=-log2(1-x),即f(x)=log2(1-x),-1≤x<0,由f(x)=log2(1-x)=a,解得x=1-2a,如图,因为函数f(x)为奇函数,所以函数F(x)=f(x)-a(0<a<1)的所有零点之和为x=1-2a.
(-x+1)=-log2(1-x),即f(x)=log2(1-x),-1≤x<0,由f(x)=log2(1-x)=a,解得x=1-2a,如图,因为函数f(x)为奇函数,所以函数F(x)=f(x)-a(0<a<1)的所有零点之和为x=1-2a.
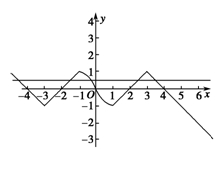
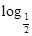 (-x+1)=-log2(1-x),即f(x)=log2(1-x),-1≤x<0,由f(x)=log2(1-x)=a,解得x=1-2a,如图,因为函数f(x)为奇函数,所以函数F(x)=f(x)-a(0<a<1)的所有零点之和为x=1-2a.
(-x+1)=-log2(1-x),即f(x)=log2(1-x),-1≤x<0,由f(x)=log2(1-x)=a,解得x=1-2a,如图,因为函数f(x)为奇函数,所以函数F(x)=f(x)-a(0<a<1)的所有零点之和为x=1-2a.

练习册系列答案
相关题目
 在
在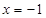 处有极值,则
处有极值,则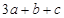 的值为 .
的值为 .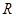 上的函数
上的函数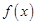 满足
满足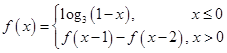 ,则
,则 .
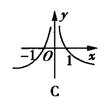
.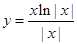 的图像可能是( )
的图像可能是( ) 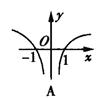


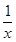 ,则f(-1)=________.
,则f(-1)=________.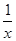 ,则f(-1)=( ).
,则f(-1)=( ).