题目内容
2．在△ABC中，A=60°，b=3，面积S=3$\sqrt{3}$，则a=$\sqrt{13}$．分析 利用三角形的面积计算公式、余弦定理即可得出．
解答 解：∵A=60°，b=3，面积S=3$\sqrt{3}$，
∴3$\sqrt{3}$=$\frac{1}{2}$×3csin60°，
解得c=4．
∴a2=b2+c2-2bccosA=32+42-2×3×4cos60°=13．
∴a=$\sqrt{13}$．
故答案为：$\sqrt{13}$．
点评 本题考查了三角形的面积计算公式、余弦定理，属于基础题．
练习册系列答案
相关题目
13．若i是虚数单位，z=1+i，则z•$\overline{z}$+|$\overline{z}$|-1=（ ）
| A． | $\sqrt{2}$+1 | B． | $\sqrt{2}$+3 | C． | 2$\sqrt{2}$-1 | D． | 2$\sqrt{2}$+1 |
10．命题p：?x0∈R使sinx0=$\frac{{\sqrt{5}}}{2}$；q：?x∈R都有x2+x+1＞0给出下列结论：
①命题“p∧q”为真；
②命题“p∧?q”为假；
②命题“￢p∨q”为真；
④命题“￢p∨￢q”为假；
其中正确的命题序号为（ ）
①命题“p∧q”为真；
②命题“p∧?q”为假；
②命题“￢p∨q”为真；
④命题“￢p∨￢q”为假；
其中正确的命题序号为（ ）
| A． | ②④ | B． | ②③ | C． | ③④ | D． | ①②③ |
7．已知函数y=f（x）是偶函数，且f（2）=5，那么f（2）+f（-2）的值为（ ）
| A． | 0 | B． | 2 | C． | 5 | D． | 10 |
11．
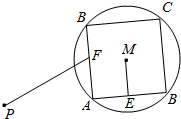如图，已知圆M的半径为2，点P与圆心M的距离为4，正方形ABCD是圆M的内接四边形，E，F是边AB，AD的中点，当正方形ABCD绕圆心M转动时，$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是（ ）
如图，已知圆M的半径为2，点P与圆心M的距离为4，正方形ABCD是圆M的内接四边形，E，F是边AB，AD的中点，当正方形ABCD绕圆心M转动时，$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是（ ）| A． | [-2，2] | B． | [-2$\sqrt{2}$，2$\sqrt{2}$] | C． | [-4，4] | D． | [-4$\sqrt{2}$，4$\sqrt{2}$] |
12．下列命题中，真命题是（ ）
| A． | ?x0∈R，ex＜0 | |
| B． | 若a，b∈R，a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| C． | 命题p：?x∈R，f（x）≥0，则?p：?x0∈R，f（x）＜0 | |
| D． | 命题“在△ABC中，若$\overrightarrow{AB}•\overrightarrow{BC}$＜0，则△ABC为钝角三角形的逆命题为真命题 |