题目内容
17.在△AOB中,G为△AOB的重心,且$∠AOB=\frac{π}{3}$.若$\overrightarrow{OA}•\overrightarrow{OB}=6$,则$|{\overrightarrow{OG}}|$的最小值是2.分析 如图所示,D为AB的中点.由$∠AOB=\frac{π}{3}$,$\overrightarrow{OA}•\overrightarrow{OB}=6$,可得$|\overrightarrow{OA}||\overrightarrow{OB}|$$cos\frac{π}{3}$=6,即$|\overrightarrow{OA}||\overrightarrow{OB}|$=12.利用三角形重心性质及其平行四边形法则可得$\overrightarrow{OG}=\frac{2}{3}$$\overrightarrow{OD}$=$\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB})$,再利用数量积性质及其基本不等式的性质即可得出.
解答 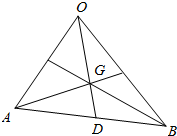 解:如图所示,
解:如图所示,
D为AB的中点.
∵$∠AOB=\frac{π}{3}$,$\overrightarrow{OA}•\overrightarrow{OB}=6$,
∴$|\overrightarrow{OA}||\overrightarrow{OB}|$$cos\frac{π}{3}$=6,即$|\overrightarrow{OA}||\overrightarrow{OB}|$=12.
∴$\overrightarrow{OG}=\frac{2}{3}$$\overrightarrow{OD}$=$\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB})$,
∴$|\overrightarrow{OG}{|}^{2}$=$\frac{1}{9}$$(|\overrightarrow{OA}{|}^{2}+|\overrightarrow{OB}{|}^{2}+12)$$≥\frac{1}{9}(2|\overrightarrow{OA}||\overrightarrow{OB}|+12)$=4,
∴$|\overrightarrow{OG}|$≥2,当且仅当$|\overrightarrow{OA}|$=$|\overrightarrow{OB}|$=2$\sqrt{3}$时取等号.
故答案为:2.
点评 本题考查了数量积的定义及其运算性质、三角形重心性质及其平行四边形法则、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案| A. | 恒小于0 | B. | 恒大于0 | C. | 可能等于0 | D. | 可正也可负 |
| A. | $\frac{3}{4}$πR2 | B. | $\frac{9}{2}$πR2 | C. | $\frac{9}{4}$πR2 | D. | $\frac{9}{8}$πR2 |
| A. | 左平移2 | B. | 左平移1 | C. | 右平移2 | D. | 右平移1 |
| A. | -1 | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -2 |