题目内容
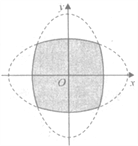
【题目】已知椭圆![]() 经过点
经过点![]() ,
, ![]() 的四个顶点构成的四边形面积为
的四个顶点构成的四边形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在椭圆![]() 上是否存在相异两点
上是否存在相异两点![]() ,使其满足:①直线
,使其满足:①直线![]() 与直线
与直线![]() 的斜率互为相反数;②线段
的斜率互为相反数;②线段![]() 的中点在
的中点在![]() 轴上,若存在,求出
轴上,若存在,求出![]() 的平分线与椭圆相交所得弦的弦长;若不存在,请说明理由.
的平分线与椭圆相交所得弦的弦长;若不存在,请说明理由.
【答案】(1)![]() (2)3
(2)3
【解析】试题分析:(1)由椭圆几何意义得![]() ,再根据A在椭圆上,列方程组,解得
,再根据A在椭圆上,列方程组,解得![]() ,(2)先设直线
,(2)先设直线![]() 的方程,并与椭圆方程联立解出E点横坐标;根据直线
的方程,并与椭圆方程联立解出E点横坐标;根据直线![]() 与直线
与直线![]() 的斜率互为相反数,可推出F点横坐标,再根据线段
的斜率互为相反数,可推出F点横坐标,再根据线段![]() 的中点在
的中点在![]() 轴上,解出直线
轴上,解出直线![]() 的斜率,最后根据几何性质得
的斜率,最后根据几何性质得![]() 的角平分线方程为
的角平分线方程为![]() .
.
试题解析:解:(1)由已知得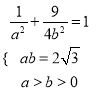 ,
,
解得![]() ,
,
∴椭圆![]() 的方程
的方程![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得
![]() .(*)
.(*)
设![]() ,
, ![]() ,且
,且![]() 是方程(*)的根,
是方程(*)的根,
∴![]() ,
,
用![]() 代替上式中的
代替上式中的![]() ,可得
,可得![]() ,
,
∵![]() 的中点在
的中点在![]() 轴上,∴
轴上,∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
因此满足条件的点![]() ,
, ![]() 存在.
存在.
由平面几何知识可知![]() 的角平分线方程为
的角平分线方程为![]() .
.
∴所求弦长为![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目