题目内容
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为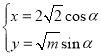 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴为非负半轴建立极坐标系,直线
轴为非负半轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;(2)4.
;(2)4.
【解析】
(1)根据极坐标与直角坐标的互化公式,即可求得直线的直角坐标方程,再由曲线的参数方程,消去参数,即可得出曲线的普通方程;
( 2)根据曲线的普通方程,由中点弦问题,利用点差法,即可求解.
(1)由题意,曲线![]() 的参数方程
的参数方程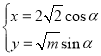 ,
,
可得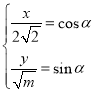 ,平方相加,即可得到曲线
,平方相加,即可得到曲线![]() 普通方程为
普通方程为![]() ,
,
又由直线![]() ,即
,即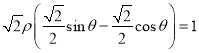 ,
,
即![]() ,根据
,根据![]() ,
,
代入可得则直线的直角坐标力程为![]() .
.
(2)依题意,线段![]() 的中点坐标
的中点坐标![]() ,
,
设![]() , 则
, 则![]() ,
,
两式相减可得![]() ,
,
整理得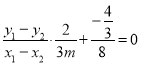 ,即
,即![]() ,解得
,解得![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 君不小于25”的概率;
君不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5填中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程,
的线性回归方程,![]() .
.
(参考公式: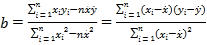 ,
,![]() ).
).