[题目]如图.侧棱与底面垂直的四棱柱ABCD.A1B1C1D1的底面是梯形.AB∥CD.AB⊥AD.AA1＝4.DC＝2AB.AB＝AD＝3.点M在棱A1B1上.且A1M＝A1B1.已知点E是直线CD上的一点.AM∥平面BC1E.(1)试确定点E的位置.并说明理由,(2)求三棱锥M-BC1E的体积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，侧棱与底面垂直的四棱柱ABCD，A1B1C1D1的底面是梯形，AB∥CD，AB⊥AD，AA1＝4，DC＝2AB，AB＝AD＝3，点M在棱A1B1上，且A1M＝A1B1.已知点E是直线CD上的一点，AM∥平面BC1E.

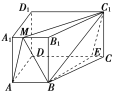
(1)试确定点E的位置，并说明理由；

(2)求三棱锥M-BC1E的体积．

【答案】（1）点E在线段CD上且EC＝1，见解析；（2）6

【解析】

（1）在上取点，使得，推导出四边形为平行四边形，从而，进而得到平面，即可确定点的位置，得到答案；

（2）由平面，得到三棱锥的体积，即可求解．

（1）点E在线段CD上且EC＝1，理由如下．

在棱C1D1上取点N，使得D1N＝A1M＝1，连接MN，DN，

又D1N∥A1M，所以,

所以四边形AMND为平行四边形，所以AM∥DN.

因为CE＝1，所以易知DN∥EC1，所以AM∥EC1，

又AM平面BC1E，EC1平面BC1E，所以AM∥平面BC1E.

故点E在线段CD上且EC＝1.

（2）由（1）知，AM∥平面BC1E，

可得

练习册系列答案

相关题目

【题目】我们把定义在上，且满足（其中常数、满足，，）的函数叫做似周期函数.

（1）若某个似周期函数满足且图象关于直线对称，求证：函数是偶函数；

（2）当，时，某个似周期函数在时的解析式为，求函数，，的解析式；

（3）对于（2）中的函数，若对任意，都有，求实数的取值范围.

【题目】已知数列满足.

（1）证明：数列为等差数列；

（2）设数列的前n项和为，若，且对任意的正整数n，都有，求整数的值；

（3）设数列满足，若，且存在正整数s，t，使得是整数，求的最小值.

【题目】某烘焙店加工一个成本为60元的蛋糕，然后以每个120元的价格出售，如果当天卖不完，剩下的这种蛋糕作餐厨垃圾处理.

（1）若烘焙店一天加工16个这种蛋糕，，求当天的利润（单位：元）关于当天需求量（单位：个，）的函数解析式；

（2）烘焙店记录了100天这种蛋糕的日需求量（单位：个），整理得下表：

日需求量	14	15	16	17	18	19	20
频数	10	20	16	16	15	13	10

①若烘焙店一天加工16个这种蛋糕，表示当天的利润（单位：元），求的分布列与数学期望及方差；

②若烘焙店一天加工16个或17个这种蛋糕，仅从获得利润大的角度考虑，你认为应加工16个还是17个？请说明理由.

【题目】中国古代计时器的发明时间不晚于战国时代(公元前476年～前222年)，其中沙漏就是古代利用机械原理设计的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道流到下部容器，如图，某沙漏由上、下两个圆锥容器组成，圆锥的底面圆的直径和高均为8 cm，细沙全部在上部时，其高度为圆锥高度的(细管长度忽略不计)．若细沙全部漏入下部后，恰好堆成一个盖住沙漏底部的圆锥形沙堆，则此圆锥形沙堆的高为(　　 )