题目内容
【题目】我们把定义在
上，且满足
（其中常数
、
满足
，
，
）的函数叫做似周期函数.
（1）若某个似周期函数
满足
且图象关于直线
对称，求证：函数
是偶函数；
（2）当，
时，某个似周期函数在
时的解析式为
，求函数，
，
的解析式；
（3）对于（2）中的函数，若对任意
，都有
，求实数
的取值范围.
【答案】（1）证明见解析；（2）
；（3）
.
【解析】
（1）利用似周期函数的性质、图像关于直线
对称，结合函数奇偶性的定义，证得
，由此证得
是偶函数.
（2）利用迭代的方法，求得，
，
的解析式.
（3）根据（2）中求得的解析式，画出图像和
的图像，确定
的大致区间，令
，求得对应
的值，由此确定的取值范围.
（1）依题意可知，函数的定义域为
，关于原点对称.由于图像关于对称，故
①.又
，即
②，用
代替得
③.由①②③可知
，而
，
，所以，故函数为偶函数.
（2）由于，
，所以
，得
.
当
时，
；
当
时，
，
；
当
时，
，
；
当
时，
，
；
……
以此类推，当
时，.
同理，由于，，所以，得
.
当
时，
，
；
当
时，
，
；
……
以此类推，当
时，
.
综上所述，当，时，
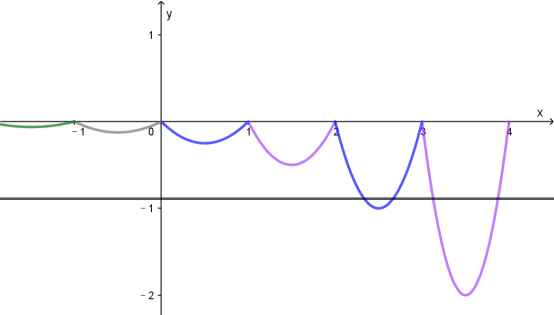
（3）由（2）画出的图像、函数图像如下图所示.由图可知，从左往右，从
开始，与图像有交点.由（2）知，当时， ；令
，解得
或
.结合图像可知，要使对任意
，都有
，则
.故的取值范围是
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
