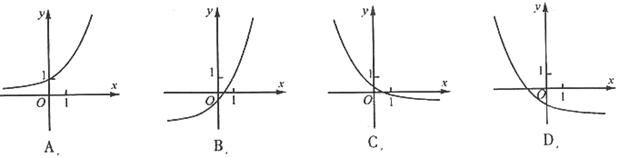
题目内容
已知函数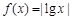 ,若
,若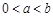 ,且
,且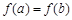 ,则
,则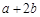 的取值范围是( )
的取值范围是( )
A.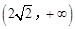 | B.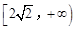 | C.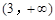 | D.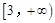 |
C
解析试题分析:因为函数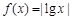
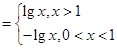 ,那么根据题意,要使得函数值相等,且有
,那么根据题意,要使得函数值相等,且有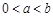 ,且
,且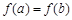 ,因此可知0<a<1,b>1,,且有-lga=lgb,则lga+lgb=1,ab=1.
,因此可知0<a<1,b>1,,且有-lga=lgb,则lga+lgb=1,ab=1.
则a+2b=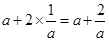 ,因为0<a<1,可知函数单调递减,故当a=1,函数接近最小值故f(x)>f(1)=3,故答案为C
,因为0<a<1,可知函数单调递减,故当a=1,函数接近最小值故f(x)>f(1)=3,故答案为C
考点:本试题考查了函数与方程的运用。
点评:解决该试题的关键是利用对数函数的图像,利用对称变换作图,然后结合函数值相等可知a,b的关系式,进而得到范围。

练习册系列答案
相关题目
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
已知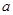 是单调函数
是单调函数 的一个零点,且
的一个零点,且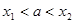 则( )
则( )
A.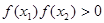 | B.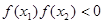 |
C.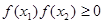 | D.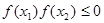 |
设函数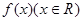 满足
满足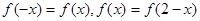 ,且当
,且当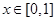 时,
时,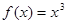 .又函数
.又函数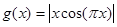 ,则函数
,则函数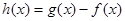 在
在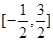 上的零点个数为 ( )
上的零点个数为 ( )
| A.5 | B. 6 | C.7 | D.8 |
定义在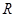 上的函数
上的函数 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若 的最小正周期是
的最小正周期是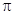 ,且当
,且当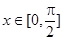 时,
时,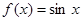 ,则
,则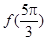 的值为( )
的值为( )
A.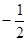 | B.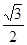 | C. | D.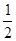 |
在函数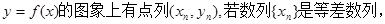 数列{
数列{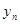 }是等比数列,则函数
}是等比数列,则函数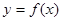 的解析式可能为( )
的解析式可能为( )
A.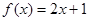 | B.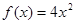 |
C.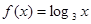 | D.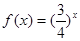 |
已知函数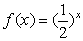 ,则函数
,则函数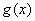 的图象与
的图象与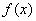 的图象关于直线
的图象关于直线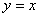 对称,则函数
对称,则函数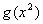 是( )
是( )
A.奇函数在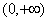 上单调递减 上单调递减 | B.偶函数在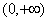 上单调递增 上单调递增 |
C.奇函数在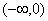 上单调递减 上单调递减 | D.偶函数在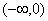 上单调递增 上单调递增 |
对实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,设函数
,设函数 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C.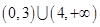 | D. |
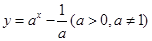 的图象可能是 ( )
的图象可能是 ( )