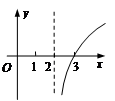题目内容
设函数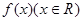 满足
满足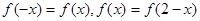 ,且当
,且当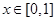 时,
时,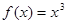 .又函数
.又函数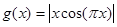 ,则函数
,则函数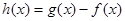 在
在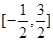 上的零点个数为 ( )
上的零点个数为 ( )
| A.5 | B. 6 | C.7 | D.8 |
B
解析试题分析:因为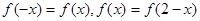 ,所以函数f(x)是奇函数,图像关于x=1对称且f(-x)=f(2-x),f(x)=f(2+x),函数周期为2.确定函数
,所以函数f(x)是奇函数,图像关于x=1对称且f(-x)=f(2-x),f(x)=f(2+x),函数周期为2.确定函数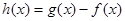 在
在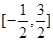 上的零点,即求
上的零点,即求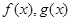 图象交点个数。
图象交点个数。
∵当x∈[0,1]时,f(x)=x³
∴当x∈[-1,0]]时,f(x)=-x³
∴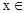 [1,
[1, 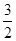 ]时,f(x)=f(x-2)=-(x-2)³
]时,f(x)=f(x-2)=-(x-2)³
g(x)=|xcos(πx)|
g(-x)=g(x),g(x)是偶函数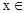 [-
[-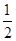 ,
,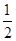 ],
], 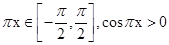
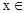 [1,
[1, 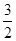 ],
], 
g(x)=-xcos(πx),
在同一坐标系内画出函数在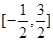 上的简图,观察交点个数为6个。
上的简图,观察交点个数为6个。
∴h(x)=g(x)-f(x)在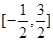 上的零点个数有6个。故选B。
上的零点个数有6个。故选B。
考点:本题主要考查零点的概念,函数的奇偶性、周期性,函数的图象。
点评:难题,这类题的一般解法是图象法。本题首先要明确函数的奇偶性、周期性,以便于作图。将问题转化成“求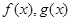 图象交点个数”是基础,正确画图是关键,本题函数g(x)=|xcos(πx)|作图较难,可定性地猜测。
图象交点个数”是基础,正确画图是关键,本题函数g(x)=|xcos(πx)|作图较难,可定性地猜测。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列各组函数是同一函数的是( )
①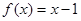 与
与 ; ②
; ②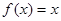 与
与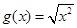 ;
;
③ 与
与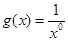 ; ④
; ④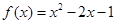 与
与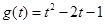 。
。
| A.①② | B.①③ | C.③④ | D.①④ |
下列函数中,值域为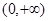 的是( )
的是( )
A.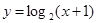 | B.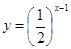 | C.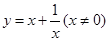 | D.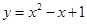 |
函数 的零点所在的区间为( )
的零点所在的区间为( )
A. | B. | C. | D. |
设 用二分法求方程
用二分法求方程 在区间(1,2)上近似解的过程中,计算得到
在区间(1,2)上近似解的过程中,计算得到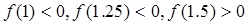 ,则方程的根落在区( )
,则方程的根落在区( )
| A.(1,1.25) | B.(1.25,1.5) | C.(1.5, 1.75) | D.(1.75,2) |
已知函数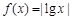 ,若
,若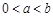 ,且
,且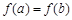 ,则
,则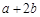 的取值范围是( )
的取值范围是( )
A.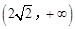 | B.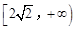 | C.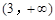 | D.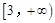 |
已知函数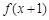 是偶函数,当
是偶函数,当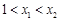 时,
时, 恒成立,设
恒成立,设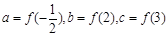 ,则
,则 的大小关系为 ( )
的大小关系为 ( )
A.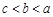 | B.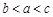 | C.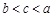 | D.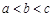 |
在区间 上不是增函数的是( )
上不是增函数的是( )
A. | B. | C. | D. |
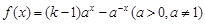 在
在 上既是奇函数,又是减函数,则
上既是奇函数,又是减函数,则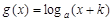 的图象是
的图象是