题目内容
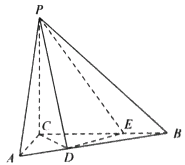
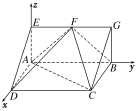
【题目】如图,三棱柱![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
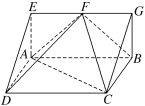
(1)求证:![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的平面角的大小.
的平面角的大小.
【答案】(1)见解析(2)![]()
【解析】
(1)先由已知面面垂直证明![]() 平面
平面![]() ,得
,得![]() ,再在矩形
,再在矩形![]() 中由勾股定理逆定理证明
中由勾股定理逆定理证明![]() ,从而可得线面垂直;
,从而可得线面垂直;
(2)由(1)知![]() ,
,![]() ,
,![]() 两两垂直,以它们为坐标轴建立空间直角坐标系,写出各点坐标,求出平面的法向量,用向量法求二面角.
两两垂直,以它们为坐标轴建立空间直角坐标系,写出各点坐标,求出平面的法向量,用向量法求二面角.
解:(1)证明:∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
又由四边形![]() 是矩形知,
是矩形知,![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() 两两垂直,分别以
两两垂直,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则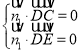 ,即
,即![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,
,
取![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∴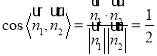 ,
,
∴锐二面角![]() 的平面角的大小是
的平面角的大小是![]() .
.

 阅读快车系列答案
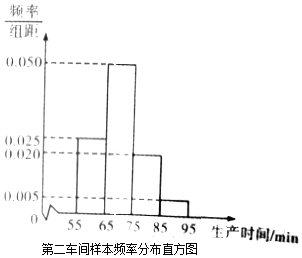
阅读快车系列答案【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
【题目】有一片产量很大的水果种植园,在临近成熟时随机摘下某品种水果100个,其质量(均在l至11kg)频数分布表如下(单位: kg):
分组 | | | | | |
频数 | 10 | 15 | 45 | 20 | 10 |
以各组数据的中间值代表这组数据的平均值,将频率视为概率.
(1)由种植经验认为,种植园内的水果质量![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .请估算该种植园内水果质量在
.请估算该种植园内水果质量在![]() 内的百分比;
内的百分比;
(2)现在从质量为![]() 的三组水果中用分层抽样方法抽取14个水果,再从这14个水果中随机抽取3个.若水果质量
的三组水果中用分层抽样方法抽取14个水果,再从这14个水果中随机抽取3个.若水果质量![]() 的水果每销售一个所获得的的利润分别为2元,4元,6元,记随机抽取的3个水果总利润为
的水果每销售一个所获得的的利润分别为2元,4元,6元,记随机抽取的3个水果总利润为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.