题目内容
若正数x,y满足x+y=1,且
+
≥4对任意x,y∈(0,1)恒成立,则正数a的取值范围是 .
| 1 |
| x |
| a |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:利用基本不等式的性质可得
+
=(x+y)(
+
)=1+a+
+
≥1+a+2
=1+a+2
,由于
+
≥4对任意x,y∈(0,1)恒成立,可得4≤(
+
)min,解出即可.
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| y |
| x |
| ax |
| y |
|
| a |
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
解答:
解:∵正数x,y满足x+y=1,
∴
+
=(x+y)(
+
)=1+a+
+
≥1+a+2
=1+a+2
,当且仅当y=
x时取等号.
∵
+
≥4对任意x,y∈(0,1)恒成立,
∴1+a+2
≥4,
化为(
)2+2
-3≥0,即(
+3)(
-1)≥0
解得a≥1.
∴正数a的取值范围是[1,+∞).
故答案为:[1,+∞).
∴
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| y |
| x |
| ax |
| y |
|
| a |
| a |
∵
| 1 |
| x |
| a |
| y |
∴1+a+2
| a |
化为(
| a |
| a |
| a |
| a |
解得a≥1.
∴正数a的取值范围是[1,+∞).
故答案为:[1,+∞).
点评:本题考查了基本不等式的性质、恒成立问题的等价转化方法、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
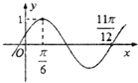 函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<
函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<| π |
| 2 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
已知等比数列{an}中,各项都是正数,且a2,
a4,2a3成等差数列,则
=( )
| 1 |
| 2 |
| a7+a8 |
| a5+a6 |
A、1+
| ||
B、1-
| ||
C、3+2
| ||
D、3-2
|
 如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.