题目内容
12.已知平行四边形ABCD的周长为18,AC=$\sqrt{65}$,BD=$\sqrt{17}$,求平行四边形的面积.分析 如图所示,设AB=x,则BC=9-x.设∠DAB=α.在△ABD与△ABC中,由余弦定理可得:BD2=(9-x)2+x2-2x(9-x)cosα,AC2=(9-x)2+x2-2x(9-x)cos(π-α),联立消去α,解出x,再利用三角形面积计算公式即可得出.
解答 解:如图所示,
设AB=x,则BC=9-x.设∠DAB=α.
在△ABD与△ABC中,由余弦定理可得:
BD2=(9-x)2+x2-2x(9-x)cosα,AC2=(9-x)2+x2-2x(9-x)cos(π-α),
∴17+65=2(9-x)2+2x2,
化为x2-9x+20=0.
解得x=4或5,
不妨设AB=5,BC=4,
∴cosα=$\frac{{5}^{2}+{4}^{2}-17}{2×5×4}$=$\frac{3}{5}$,
∴$sinα=\frac{4}{5}$.
∴平行四边形的面积S=$5×4×\frac{4}{5}$=16.
点评 本题考查了平行四边形的性质、余弦定理、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.已知复数z=$\frac{2}{1+\sqrt{3}i}$,则|$\overline{z}$|等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | 1 | D. | $\sqrt{2}$ |
 如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20152的格点的坐标为(1008,1007).
如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20152的格点的坐标为(1008,1007).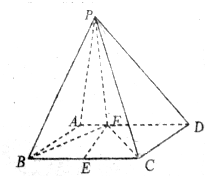 如图,四棱锥P-ABCD的地面ABCD是平行四边形,PF⊥平面ABCD,垂足F在AD上,且AF=$\frac{1}{3}$FD,FB⊥FC,FB=FC=2,PF=4,E是BC的中点.
如图,四棱锥P-ABCD的地面ABCD是平行四边形,PF⊥平面ABCD,垂足F在AD上,且AF=$\frac{1}{3}$FD,FB⊥FC,FB=FC=2,PF=4,E是BC的中点.