题目内容
4. 如图,四棱锥P-ABCD的地面ABCD是平行四边形,PF⊥平面ABCD,垂足F在AD上,且AF=$\frac{1}{3}$FD,FB⊥FC,FB=FC=2,PF=4,E是BC的中点.
如图,四棱锥P-ABCD的地面ABCD是平行四边形,PF⊥平面ABCD,垂足F在AD上,且AF=$\frac{1}{3}$FD,FB⊥FC,FB=FC=2,PF=4,E是BC的中点.(1)求异面直线EF与PC所成角的大小
(2)求点D到平面PBF的距离.
分析 (1)利用平行关系作出异面直线EF与PC所成的角;
(2)利用几何关系找出点D到PBF的距离
解答 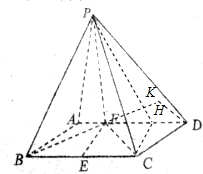 解:(1)在平面ABCD内,过C做CH∥EF,交AD于H,连接PH
解:(1)在平面ABCD内,过C做CH∥EF,交AD于H,连接PH
则∠PCH(或其补角)就是异面直线EF与PC所成的角
在△PCH中,CH=$\sqrt{2}$,PC=$\sqrt{20}$,PH=$\sqrt{18}$,
由余弦定理可得cos∠PCH=$\frac{\sqrt{10}}{10}$
∴异面直线EF和PC所成的角为arccos$\frac{\sqrt{10}}{10}$;
(2)∵PF⊥平面ABCD,PF?平面PBA
∴平面PBF⊥平面ABCD
在平面ABCD内过D作DK⊥BF,交BF延长线与K,则DK⊥平面PBF
∴DK的长就是点D到平面PBF的距离
∵BC=2$\sqrt{2}$
∴DF=$\frac{3}{4}$AD=$\frac{3}{4}$BC=$\frac{3}{2}$$\sqrt{2}$,
∵在△DFK中DK=DFsin45°=$\frac{3}{2}$
∴点D到平面PBF的距离为$\frac{3}{2}$.
点评 此题考查了运用定义法来求异面直线的夹角和点到面的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.设f(x)是定义在R上的不恒为零的偶函数,且对任意的实数x都有xf(x+1)=(1+x)f(x)-x,则f($\frac{3}{2}$)的值为( )
| A. | -$\frac{5}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
9.若$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=2tanα恒成立,则角α可能在的象限是( )
| A. | 第一象限 | B. | 第四象限 | C. | 第一、四象限 | D. | 第二、三象限 |
16.已知A,B,C是△ABC的三内角,且满足2cosBcosC(1-tanBtanC)=1,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
