题目内容
【题目】如图所示,正方体ABCD﹣A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1 , BB1的中点.
(1)画出过M,N,P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线;
(2)设过M,N,P三点的平面与B1C1交于Q,求PQ的长.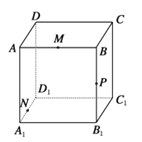
【答案】解:(1)如图所示:∵MP平面ABB1 ,
∴MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上,
∴过点M,N,P的平面与平面ABCD的交线是NK,(K在线段AB的延长线上),与平面BB1C1C的交线是PQ(Q在线段BC上).∵BK∥A1B1 ,
∴![]() =
=![]() =1,∴BK=4.
=1,∴BK=4.
∵BQ∥AN,∴![]() =
=![]() =
=![]() ,
,
∴BQ=![]() .
.
(2)由(1)可知:BQ=![]() ,BP=4,在Rt△BPQ中,由勾股定理得PQ=
,BP=4,在Rt△BPQ中,由勾股定理得PQ=![]() =
=![]()
![]() .
.
【解析】(1)根据MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上,连接NK交BC与Q,与平面BB1C1C的交线是PQ.
(2)根据(1)得到的交线PQ,在Rt△BPQ中,由勾股定理可求得.

练习册系列答案
相关题目