题目内容
【题目】(本题满分10分)
已知椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,离心率
,离心率![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .求证:以
.求证:以![]() 为直径的圆恒过一定点
为直径的圆恒过一定点![]() .并求出点
.并求出点![]() 的坐标.
的坐标.
【答案】(1)![]() =1(2)存在定点M(1,0),
=1(2)存在定点M(1,0),
【解析】试题分析:(Ⅰ)根据过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() 的周长为8,可得
的周长为8,可得![]() ,即
,即![]() ,利用
,利用![]() ,
, ![]() ,即可求得椭圆E的方程.(Ⅱ)由
,即可求得椭圆E的方程.(Ⅱ)由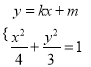 消元可得
消元可得![]() ,利用动直线
,利用动直线![]() 与椭圆E有且只有一个公共点
与椭圆E有且只有一个公共点![]() ,可得
,可得![]() ,进而可得
,进而可得![]() ,由
,由![]() 得
得![]() ,取
,取![]()
![]() ,猜想满足条件的点
,猜想满足条件的点![]() 存在,只能是
存在,只能是![]() ,再进行证明即可
,再进行证明即可
试题解析:(1)∵![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() .
.
又因为![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(2)法一:由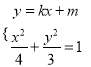 消去
消去![]() 得
得![]() .
.
因为动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,所以
,所以![]() ,且
,且![]() ,即
,即
![]() ,化简得
,化简得![]() .
.
此时![]() ,
, ![]() ,所以
,所以![]()
由![]() 得
得![]()
从而以线段![]() 为直径的圆的方程满足
为直径的圆的方程满足![]() ,化简得
,化简得
![]() .
.
由对称性知,点![]() 必在
必在![]() 轴上.而当
轴上.而当![]() 时,
时, ![]() ,易得
,易得![]() ,此式恒成立.
,此式恒成立.
故命题成立.定点坐标为![]() .
.
法二:由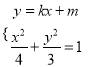 消去
消去![]() 得
得![]() .
.
因为动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,所以
,所以![]() ,且
,且![]() ,即
,即
![]() ,化简得
,化简得![]() .
.
此时![]() ,
, ![]() ,所以
,所以![]()
由![]() 得
得![]() .
.
因为存在定点![]() 满足条件,由图形对称性知:点
满足条件,由图形对称性知:点![]() 必在
必在![]() 轴上.取
轴上.取![]()
此时![]() 以
以![]() 为直径的圆的方程为
为直径的圆的方程为![]() 交
交![]() 轴于
轴于![]() ,
,![]() ;取
;取![]() ,此时
,此时![]() ,以
,以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,交
,交![]() 轴于点
轴于点![]() .所以满足条件的点存在,其必为
.所以满足条件的点存在,其必为![]() .
.
下面证明点![]() 满足条件.
满足条件.
因为![]() 所以
所以![]() ,故
,故
恒有![]() ,故点
,故点![]() 恒在以线段
恒在以线段![]() 为直径的圆上.
为直径的圆上.

练习册系列答案
相关题目