Question

【题目】已知定义域为R的函数f（x）=是奇函数．
（1）求a，b的值；
（2）判断函数f（x）的单调性，并用定义证明；
（3）若对于任意都有f（kx2）+f（2x﹣1）＞0成立，求实数k的取值范围．

Answer 1

【答案】解：（1）因为f（x）是奇函数，所以f（0）=0=0，解得b=1，
f（x）=，又由f（1）=﹣f（﹣1）=，解得a=2．
（2）证明：由（1）可得：f（x）==．
x1＜x2 ， ∴＞0，
则f（x1）﹣f（x2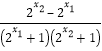）==＞0，
∴f（x1）＞f（x2）．
∴f（x）在R上是减函数．
（3）∵函数f（x）是奇函数．
∴f（kx2）+f（2x﹣1）＞0成立，等价于f（kx2）＞﹣f（2x﹣1）=f（1﹣2x）成立，
∵f（x）在R上是减函数，∴kx2＜1﹣2x，
∴对于任意都有kx2＜1﹣2x成立，
∴对于任意都有k＜，
设g（x）=，
∴g（x）==，
令t=，t∈[，2]，
则有,，∴g（x）min=g（t）min=g（1）=﹣1
∴k＜﹣1，即k的取值范围为（﹣∞，﹣1）
【解析】（1）直接根据函数是奇函数，满足f（﹣x）=﹣f（x），把x=0，和x=1代入，即可得到关于a，b的两个等式，解方程组求出a，b的值．
（2）利用减函数的定义即可证明．
（3））f（kx2）+f（2x﹣1）＞0成立，等价于f（kx2）＞﹣f（2x﹣1）=f（1﹣2x），即k＜成立，设g（x）= ，
换元使之成为二次函数，再求最小值．